1.旋转因子

通常把模为1的复数ejθ=1∠θ 称为旋转因子。

取任意复数

则

即任意复数乘以旋转因子后，其模不变，辐角在原来的基础上增加了θ，这就相当于把该复数矢量逆时针旋转了θ 角，这一点我们从图4-15中可以明显地看出。

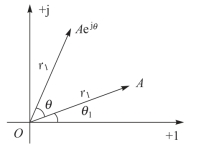
图4-15　旋转因子

2.正弦量的旋转矢量表示法

旋转因子1∠θ 的辐角θ 为一常量，此时任意复数乘以该旋转因子后就会旋转θ 角。假使θ=ω t是一个随时间匀速变化的角，其角速度为ω，不难想象，若任意复数乘以这个旋转因子ejωt=1∠ω t后，其复数矢量就会在原来的基础上逆时针旋转起来，且旋转的角速度也是ω。

假设有一个正弦电流i=Imsin （ω t+ψ），在复平面上过原点作一个矢量，如图4-16所示。矢量与横轴正方向的夹角等于正弦电流的初相ψ，它的长度等于正弦电流的最大值Im，并令矢量以角速度ω 逆时针旋转，旋转中的矢量在纵轴的投影是变化的。当t=0时，该矢量在纵轴上的投影oa=Imsin ψ。经过t1时间，矢量旋转的角度为ω t1，与横轴的夹角为 （ω t1+ψ），它在纵轴的投影ob=Imsin （ω t1+ψ），刚好等于正弦电流在t1时刻的瞬时值。因此，在任意时刻，以角速度ω 逆时针旋转的矢量在纵轴上的投影，都与正弦电流在该时刻的瞬时值保持一一相等的对应关系。像这样旋转的矢量，称为旋转矢量（rotating phasor）。旋转矢量既能反映正弦量的三要素，又能通过它在纵轴上的投影确定正弦量的瞬时值，所以复平面上的一个旋转矢量可以完整地表示一个正弦量。这也是正弦量的一种表示方法。

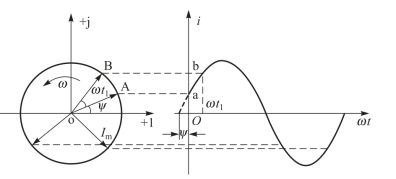
图4-16　正弦量的复数表示

复平面上的矢量与复数是一一对应的，用复数Imejψ来表示复数的起始位置，再乘以旋转因子ejωt便为上述旋转矢量，即

该矢量的虚部即为正弦量的解析式，这与旋转矢量的纵轴投影为正弦量的瞬时值是同样意思。由于复数本身并不等于正弦函数，因此用复数可以相对应地表示一个正弦量，但两者并不相等。

3.正弦量的相量表示

正弦量的相量表示

在正弦交流电路中，若输入的信号（称激励）是角频率为ω 的正弦量，则电路中任何一处的电压、电流（称响应）均为同角频率ω 的正弦量，表示它们的那些旋转矢量的角速度相同，相对位置不变，可以不考虑它们的旋转，只用起始位置的矢量来表示正弦量，即把旋转因子ejωt省去，而用复数Imejψ对应地表示正弦量i。

这种能表示正弦量的特征的复数就称为相量（phasor），规定相量用上面带小圆点的大写字母来表示，如表示电流相量，表示电压相量。所加的小圆点表示它是对应某一正弦的时间函数，以与一般的复数相区别。这就是正弦量的相量表示法。(www.daowen.com)

正弦电流i=Imsin （ω t+ψi）的相量，可以写成

相量的模是正弦量的振幅，故称为电流的振幅相量。

同理，正弦电压u=Umsin （ω t+ψu） 的振幅相量为

由于电路分析中往往有效值比最大值更为常用，因而使用更多的是有效值相量，即

电流相量

电压相量

今后若未特殊说明，正弦量的相量就是指有效值相量。

值得注意的是，用相量表示正弦量是指两者有对应关系，而不是指两者相等。正弦量是时间的函数，而相量只是与正弦量的大小（振幅值或有效值）及初相相对应的复数。

4.正弦量的相量图

正弦量的相量图

相量只能表示正弦量三要素中的两个，角频率需另加说明。只有同频率的正弦量其相量才能画在同一复平面上，画在同一复平面上表示相量的图称为相量图。

画几个同频率正弦量的相量图时，可选择某一相量为参考相量先画出，再根据其他正弦量与参考正弦量的相位差画出其他相量。参考相量的位置可以根据需要，任意选择。

例4.9 正弦电压u=141sin （ω t-30°） V，正弦电流i=14.14sin （ω t+135°） A，写出u和i的相量，画出相量图，并比较两正弦量超前、滞后关系。

解：电压相量U˙=100∠-30°V；

电流相量I˙=10∠135°A。

它们的相量图如图 4-17 所示。由图可见，超前165°。

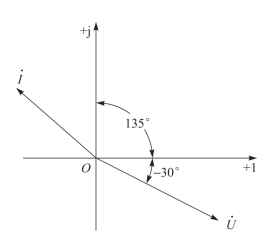
图4-17　例4.9 相量图

应注意的是，在同一相量图中，各相量所表示的正弦电量必须是同频率的正弦量。只有这样，才能对各个正弦量进行相位关系的比较。在同一个相量图中不能表示不同频率的正弦量。