1.复数

在数学中用A=a+bi表示复数，其中a为实部，b为虚部，i=称为虚数单位。在电气工程中，为区别于电流的符号，虚数单位常用j代替i，复数常用A=a+jb表示。

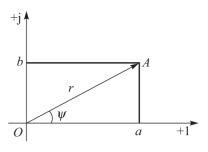
图4-11　复数的表示

用直角坐标的横轴表示实轴，以+1为单位；纵轴表示虚轴，以+j为单位。实轴和虚轴构成复坐标平面，简称复平面。于是任何一个复数就与复平面上的一个确定点相对应。例如复数A=a+jb与复平面上A（a，b）点相对应，如图4-11所示。再用有向线段连接坐标原点O和点A，在线段末端带有箭头，成为一个矢量，该矢量就与复数A对应。这种表示复数的矢量称为复矢量。复矢量OA的长度r为复数的模，即

复矢量OA和实轴正方向的夹角ψ 称为复数A的辐角，即

不难看出，复数A的模在实轴上的投影就是复数A的实部，在虚轴上的投影就是复数A的虚部，即

2.复数的四种表示形式

（1）复数的代数形式。

（2）复数的三角函数形式。

（3）复数的指数形式。

根据欧拉公式

可得到复数的指数形式为

（4）复数的极坐标形式。

在电路中，复数的模和辐角通常用更简明的极坐标形式表示

在以后的运算中，经常会用到复数的代数形式和极坐标形式，它们之间的换算应十分熟练。

例4.6 写出复数A1=4-j3，A2=-3+j4的指数形式和极坐标形式。

例4.7 写出1，-1，j，-j的极坐标式，并在复平面内做出其矢量图。解：复数1的实部为1，虚部为0，其极坐标式为 1=1∠0°；复数-1的实部为-1，虚部为0，其极坐标式为(www.daowen.com)

复数j的实部为0，虚部为1，其极坐标式为

复数-j的实部为0，虚部为-1，其极坐标式为

矢量图如图4-12所示，这四个复数的代数式和极坐标式的互换在后续课程中常用，望牢固掌握。

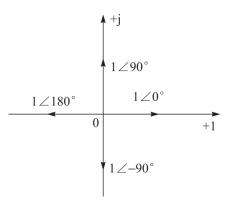
图4-12　例4.7矢量图

3.复数的四则运算

（1）复数的加减法。

复数的加、减运算应用代数形式较为方便。设有两个复数：

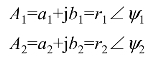
则

即复数相加减时，将实部和实部相加减，虚部和虚部相加减。图4-13为复数相加减矢量图。复数相加符合“平行四边形法则”，复数相减符合“三角形法则”。

（2）复数的乘除法。

复数相乘或相除时，以指数形式和极坐标式表示较方便。

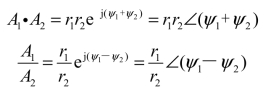
即复数相乘，模相乘，辐角相加；复数相除，模相除，辐角相减。

例4.8 已知复数A1=6+j8，A2=8-j6。求

解：

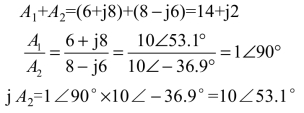
若复数A=r∠ψ 乘以j，则为jA=r∠（ψ+90°）。这表明，任意一个复数乘以j，其模值不变，辐角增加90°，相当于在复平面上把复数矢量逆时针旋转90°，如图4-14所示。因此，j称为旋转90°的因子。

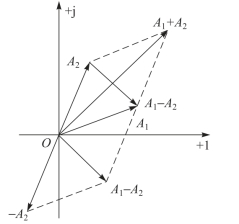
图4-13　复数相加减矢量图

图4-14　复数A乘以j的几何意义