从以上求解一阶电路的全响应中可知:在外加直流电源激励下的非零初始状态的一阶电 路中,各处的电压和电流都是从其初始值开始,按指数![]() 规律衰减或增长到稳态值的,而且在同一电路中,各处的电压和电流变化的时间常数τ都是相同的。因此,在上述一阶电路中,任意电压或电流都是由其初始值、稳态值和时间常数这三个参数确定的。若用f (t)表示一阶电路中的响应(电压或电流),f(0+) 表示其初始值,f(∞)表示其稳态值,τ 表示电路的时间常数,则一阶电路中的响应f(t)可表示为
规律衰减或增长到稳态值的,而且在同一电路中,各处的电压和电流变化的时间常数τ都是相同的。因此,在上述一阶电路中,任意电压或电流都是由其初始值、稳态值和时间常数这三个参数确定的。若用f (t)表示一阶电路中的响应(电压或电流),f(0+) 表示其初始值,f(∞)表示其稳态值,τ 表示电路的时间常数,则一阶电路中的响应f(t)可表示为

一阶电路的 三要素法
![]()
式(3.58)中,f(0+)、f(∞)和τ 通常称为一阶电路的三要素,利用这三个要素可直接求出在直流电源激励下的一阶电路任一电压或电流的响应,这种方法就称为分析一阶电路响应的三要素法(three elements method)。式(3.58)为三要素法公式。
由于零输入响应和零状态响应是全响应的特殊情况,故式(3.58)同样适应于求解一阶电路的零输入响应和零状态响应。
分析一阶电路响应的三要素法,只要求计算出响应的初始值、稳态值和时间常数,即可直接写出一阶电路任一电压或电流的响应表达式,故求解一阶电路的响应问题就转化成求解三要素的问题。其步骤如下:
① 确定初始值:初始值f(0+)是指任一响应换路后瞬间t=0+时的值,其求法见3.3.3节。
② 确定稳态值:稳态值f(∞)是指任一响应在换路后电路达到稳态时的值,其求法可画出t=∞时的等效电路。稳态时对于直流电源激励下一阶电路,电容相当于开路,电感相当于短路,按照求解直流电路的方法求解出响应的值,即为稳态值。
③求时间常数:RC电路中,τ=ROC;RL电路中,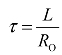 。其中,RO是将电路中所有独立源置零后,从电容或电感两端看进去的等效电阻(即戴维南等效电阻)。
。其中,RO是将电路中所有独立源置零后,从电容或电感两端看进去的等效电阻(即戴维南等效电阻)。
例3.12 试用三要素法求解例3.11。
解:①确定初始值:由于t<0时,电感电流的初始值iL(0-)=0,由换路定律,可得t=0+时的电感电流
![]()
表明换路瞬间电感相当于开路。故
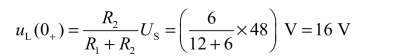
② 确定稳态值:显然当t=∞时,电感相当于短路,故得
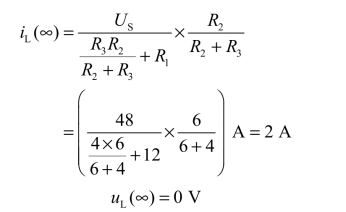
③求时间常数:求法见例3.11。即
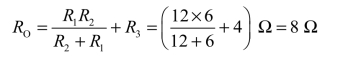
电路的时间常数为
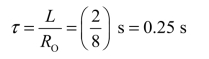 (www.daowen.com)
(www.daowen.com)
分别将iL和uL的初始值、稳态值和时间常数代入式(3.58)中,得
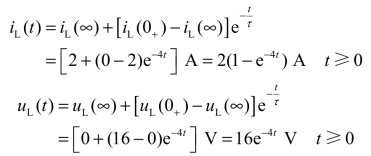
显然结果同例3.11。
例3.13 图3-26(a)所示电路中,设t<0时开关S断开已久,在t=0时开关S闭合。试求t≥0时的i(t)。
解:①确定初始值:开关S闭合前瞬间,电感相当于短路,电感电流为
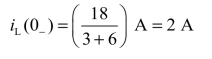
由换路定律,得
![]()
画出如图3-26(b)所示的t=0+等效电路,利用叠加定理可求得
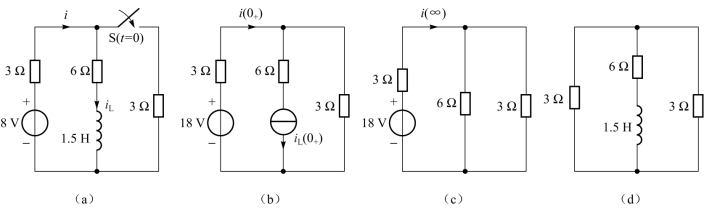
图3-26 例3.13图
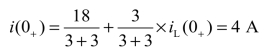
② 确定稳态值:当t=∞时,电感相当于短路,画出t=∞时如图3-26(c)所示等效电路。易求得
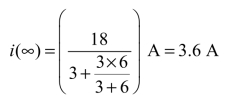
③求时间常数:将电路中电压源置零,相当于短路,如图3-26(d)所示。从电感两端看进去的等效电阻为
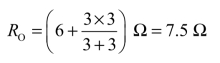
故得电路的时间常数
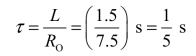
将i(t)的初始值、稳态值和时间常数代入式(3.58)中,得
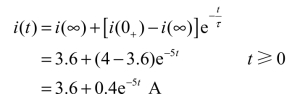
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。








