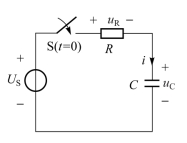
图3-24　RC电路的全响应

前面我们讨论了一阶电路的零输入响应和零状态响应。当一个非零初始状态的一阶电路外加激励时，电路中所产生的响应称为全响应（complete response）。

图3-24电路中，设直流电压源US在t=0时接入电路，显然电路中的响应为全响应。换路后 （t≥0） 以电容电压uC为电路变量，列出描述电容电压uC的微分方程为

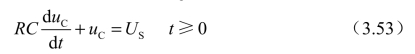
显然，式（3.53）与RC电路的零状态响应电路的微分方程式（3.35）完全相同，其解的形式必然相同，即

代入初始条件uC（0+）=uC（0-）=U0，得

故得电路电容电压的全响应为

并得电阻电压、电流的全响应分别为

(www.daowen.com)

通过对式（3.53）微分方程的分析可知，当US=0时，即为RC电路的零输入响应的微分方程；当uC（0+）=0时，即为RC电路的零状态响应的微分方程。这表明零输入响应和零状态响应都是全响应的一种特殊情况。

下面，以uC为例介绍对任何线性一阶电路的全响应都适用的两种分解方法。

①全响应分解为暂态响应和稳态响应之和。式（3.54）可分为两项，第一项为uC的齐次解，它是按指数规律衰减变化的，其规律取决于电路的特性，与激励的形式无关，当t→∞时，其值为零。故称之为暂态响应（自由响应）；第二项US为uC的特解，显然取决于激励的形式，一般情况下，当t→∞时，其值不为零。故称之为稳态响应（强制响应）。即电路的全响应可表示为

② 全响应分解为零输入响应和零状态响应之和。将式（3.54）改写为

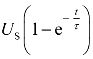式（3.57）中第一项是零输入响应（令US=0），第二项是零状态响应［令uC（0+）=U0=0］。可见电路的全响应等于零输入响应与零状态响应之和。即

全响应=零状态响应+零输入响应

这体现了线性电路的叠加性。零输入响应是由非零初始状态产生的，零状态响应是由外加激励产生的。

把全响应分解为稳态响应和暂态响应，能较明显地反映电路的工作状态，便于分析过渡过程的特点。把全响应分解为零输入响应和零状态响应，明显反映了响应与激励在能量方面的因果关系，并且便于计算。但电路真实显现出来的是全响应。

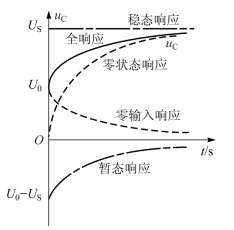
图3-25　RC电路uC的全响应波形

一阶RC电路的全响应uC曲线（设US＞U0）如图3-25所示。从图中可见，按零输入响应和零状态响应相加与按稳态响应和暂态响应相加，所得的全响应是一致的。