如图3-21（a）所示一阶RL电路，US为直流电压源，开关S闭合前，即t＜0时，电感电流为零，故称电感处于“零初始状态”。在t=0时刻开关S闭合，电路进入过渡过程。

开关S闭合后瞬间，根据换路定律，得

上式表明电感在换路瞬间相当于断路。t≥0时，直流电压源US与电路接通，电感电流iL由零初始值逐渐增加，电阻电压uR逐渐增加，当t→∞时，电感电流等于时，电路进入新的稳态，此时，称为稳态值，过渡过程结束。

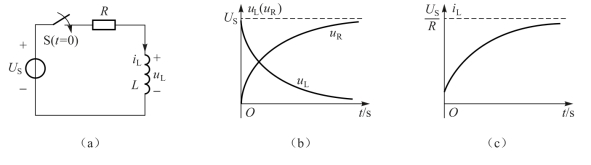
图3-21　一阶RL电路的零状态响应

其过程可作如下数学分析。

当t≥0时，根据KVL及电阻、电感的VAR可得

整理可得

初始条件为

式（3.44）是一阶线性非齐次常微分方程。其通解同样由齐次微分方程的通解iLh和特解iLp组成，即

同一阶RC电路的零状态响应解法相同，可得

式（3.46）中k为待定的积分常数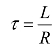，为时间常数，显然与激励形式无关。

设特解iLp=A，代入式（3.44）得

则式（3.45）一阶线性非齐次常微分方程的解为

将初始条件iL（0+）=0代入到式（3.48），求得积分常数k=，所以

由于稳态值iL（∞）=，式（3.49）也可写成

电路中的电感和电阻上的电压为

(www.daowen.com)

由式（3.50）、式（3.51）和式（3.52）可画出uR、uL和iL的变化波形，如图3-21（b）和图3-21（c）所示。由图3-21（b）可见，t=0时刻换路后，电感电压从初始值uL（0+）=US开始按指数规律衰减，当t→∞时，进入稳态，其稳态值uL（∞）=0；电阻电压uR按指数规律增加，当进入稳态时，电感相当于短路，故电阻电压uR（∞）=US。由图3-21（c）可见，t=0时刻开关S闭合后，电感电流从初始值iL（0+）=0开始按指数规律增加，当t→∞时，进入稳态，其稳态值

例3.10 图示3-22（a）电路中，设开关S闭合前电路已达稳态，在t=0时开关S闭合。已知US=10 V、R1=2 kΩ、R2=3 kΩ、R3=0.8 k Ω、C=10 μF 。试求t≥0时的uC。

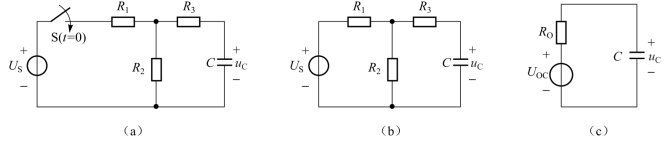
图3-22　例3.10电路

解：开关S闭合前瞬间电容电压初始值uC（0-）=0，则由换路定律可得开关S闭合后瞬间电容电压为

开关S闭合后（t≥0），电路如图3-22（b）所示，利用戴维南定理，易求得电容C两端看进去的戴维南等效电路，如图3-22（c）所示。

电路的时间常数

代入式（3.40）可得

例3.11 图示3-23（a）电路中，设开关S闭合前电路已达稳态，在t=0时开关S闭合。已知US=48 V、R1=12 Ω、R2=6 Ω、R3=4 Ω、L=2 H。试求t≥0时的uL和iL。

图3-23　例3.11电路

解：t＜0时，电感电流的初始值iL（0-）=0，由换路定律，可得t=0+时的电感电流

开关S闭合后（t≥0），电路如图3-23（b）所示，利用戴维南定理，易求得电感L两端看进去的戴维南等效电路，如图3-23（c）所示。

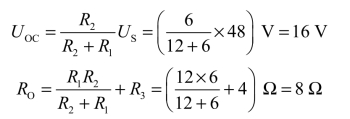
电路的时间常数为

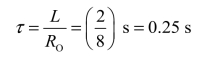
代入式（3.49）和式（3.51）可得

因此可总结一阶电路的零状态响应f（t）的求法归纳为以下步骤：

①求出换路后电容元件或电感元件两端看进去的戴维南等效电路，即求出开路电压UOC和戴维南等效电阻RO。

② 利用戴维南等效电路求出时间常数τ=ROC或τ=L/RO。

③由式（3.41）和式（3.50）写出uC（t）和iL（t）表达式。

④ 求出uC（t）和iL（t）后，再利用KVL、KCL、欧姆定律和元件的VAR求出其他支路电压和电流的零状态响应f（t）。