如图3-15（a）所示RC电路中，如在t＜0时开关S打到位置“1”，电源US通过电阻RS对电容充电，直至uC（t）=US时电路处于稳态。在t=0时刻，开关S的位置由“1”掷到“2”，电路进入过渡过程。换路前，电容已储存有初始储能，当t＞0后，电源US失去作用，电容将通过电阻R放电，直至uC（t）=0时电路进入新的稳态。电路中无独立源（激励）作用，电路的响应均是由电容元件的初始储能引起的，故属于零输入响应。

其零输入响应可作如下数学分析：

由于，在换路瞬间，电容电压不能跃变，由换路定律可得初始条件当t=0时刻，开关S断开时，其电路如图3-15（b）所示。根据KVL及电阻、电容的VAR可得

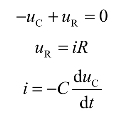
整理可得

图3-15　一阶RC电路的零输入响应

式（3.20）是一阶线性常微分齐次方程。其通解形式为

式（3.21）k为待定的积分常数，可由初始条件uC（0+）确定。p为式（3.20）对应的特征方程的根。将式（3.21）代入式（3.20）可得特征方程为

解之特征根为(www.daowen.com)

故得式（3.20）一阶线性常微分齐次方程的通解为

将初始条件uC（0+）=US代入式（3.22），求得待定的积分常数

最后得到满足初始值的一阶线性常微分齐次方程的解为

电路中的放电电流为

令τ=RC，它具有时间的量纲，即当C用法拉（F），R用欧姆（Ω）为单位时，τ 的单位为秒（s）。故称τ为时间常数（time constant），这样式（3.23）和式（3.24）可改写为

它们的响应变化波形如图3-15（c）和图3-15（d）所示。由图可见，在换路后，电容电压和电流分别由各自的初始值随时间t的增大按相同的指数规律衰减变化，当t→∞时衰减到零，达到稳定状态[uC（∞）=0，i（∞）=0]，这一变化过程称为过渡过程或暂态过程。显然电压和电流衰减的快慢取决于时间常数 τ 的大小，τ 越大，电压、电流衰减得越慢；τ 越小，电压、电流衰减的越快。以电压为例，当t=τ时，，即时间常数τ 等于零输入响应衰减到初始值的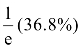所经历的时间。故电容电压uC（t）下降到约为初始值US的36.8%时所经历的时间就等于时间常数τ；当t=4τ时，电压已下降到初始值US的1.83%。理论上，只有t=∞时才能衰减为零，但在工程上一般认为，换路时间经3τ～5τ 后，此时电压已衰减至0.05US～0.006 7US，电压值基本上与稳态值接近，放电过程便基本结束。