换路定律表明电容电压或电感电流从一个数值到另一个数值必定是一个连续变化的过程。在随后的讨论中将看到,换路定律在暂态分析中的作用是为电路的微分方程的解提供初始条件。事实上,可以利用换路定律由电路在换路前一瞬间t=0-时的电容电压uC(0-)或电感电流iL(0-)完全确定换路后一瞬间t=0+时电路中的电压和电流。初始值(initial value)的计算可按如下步骤进行:
①首先根据换路前的稳态电路求出t=0-时,电路中的电容电压uC(0-)和电感电流iL(0-),然后再利用换路定律uC(0+)=uC(0-)、iL(0+)=iL(0-),确定出t=0+时的电容电压 uC(0+)和电感电流iL(0+)。
② 根据换路后的电路,将电容元件和电感元件分别用电压源和电流源代替,其值分别等于uC(0+)和iL(0+),画出t=0+时刻的等效电路。
③根据t=0+时刻的等效电路,利用KCL、KVL和欧姆定律求出电路中其他元件或支路上的电压或电流的初始值u(0+)和i(0+)。注意,独立源则取t=0+时的值。
例3.6 图示3-13(a)电路中,设开关S在t=0时断开,断开前电路已处于稳态,已知US=8 V,R1=6 Ω、R2=2 Ω、R3=2 Ω、C=1 F。求t=0+时的i1、i2、i3和uC。

初始值的计算
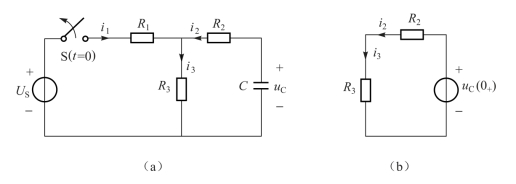
图3-13 例3.6电路
解:①确定初始值uC(0+)。由于开关S断开前电路已处于稳态,所以电容相当于开路。故有
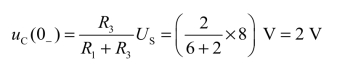
由换路定律得
![]()
② 换路后一瞬间将电容用电压源代替,其值等于uC(0+)=2 V,画出t=0+时刻的等效电路如图3-13(b)所示。
③求出相关初始值。由图3-13(b)可求得(www.daowen.com)
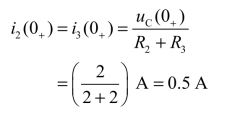
显然
![]()
由计算结果可以看出:除了电容电压和电感电流的初始值不能跃变,其他初始值可能跃变也可能不跃变。如电容上电流由零跃变到0.5 A,电阻R1的电流由1 A跃变到零。
例3.7 图示3-14(a)电路中,设开关S在t=0时闭合,闭合前电路已处于稳态,求t=0+时的i1、i2、iL、iC、uL和uC。
解:①首先确定初始值uC(0+)和iL(0+)。由于开关S闭合前电路已处于稳态,所以电容相当于开路,电感相当于短路。故有
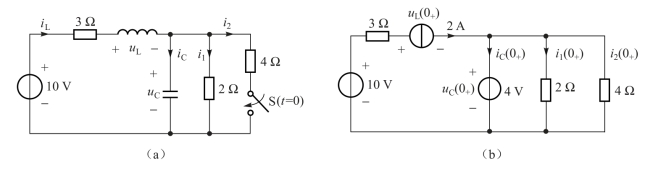
图3-14 例3.7电路
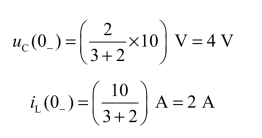
由换路定律得
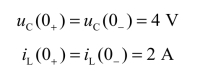
② 换路后一瞬间,将电容用值等于uC(0+)=4 V 的电压源代替,电感用值等于iL(0+)=2 A 的电流源代替,画出t=0+时刻的等效电路如图3-14(b)所示。
③求出相关初始值。由图3-14(b)可求得
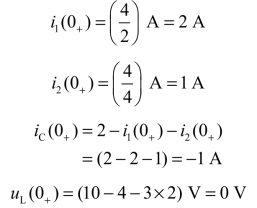
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






