含有电感或电容的动态电路的一个重要特征是当电路的结构、元件的参数或电源发生变化时，可能使电路改变原来的工作状态，进而转变到另一个工作状态，这种转变往往需要经历一个过程，即过渡过程。

从3.1节和3.2节中讨论的电容元件和电感元件可知，这两种元件的伏安关系是关于时间的微分或积分关系。因此，在分析动态电路的过渡过程时，根据KCL和KVL以及元件的VAR建立的电路方程是以电流和电压为变量的微分方程。也就是说，动态电路的数学模型是微分方程，分析动态电路的过渡过程实际上就是求解微分方程，求解微分方程必须知道初始条件，否则无法求解出微分方程的解。由于动态电路中的变量是电压或电流，因此，动态电路的初始条件就是待求电压或电流的初始值。确定电压、电流的初始值是对动态电路进行暂态分析的一个重要环节。为了求解初始条件，我们引入了换路定律（switching law）。

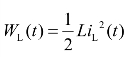分析电路的过渡过程时，为了研究方便，一般认为换路是在t=0时刻进行的。用t=0-表示换路前瞬间，t＝0＋表示换路后瞬间，换路所经历的时间为t=0-到t=0＋。换路时，电路中电容元件储存的电场能和电感元件储存的磁场能不能突变，由此可知电容电压和电感电流不能突变，即在换路时，电容上电压和电感电流在换路前瞬间和换路后瞬间的值相等。因此，换路定律可表示为

换路定律

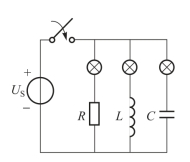
图3-12　例3.5 电路(www.daowen.com)

例3.5 电路如图3-12所示，当开关闭合时，分析电路中的三个灯的变化过程。

解：①当开关闭合后，由于电阻元件不是储能元件，该支路不存在过渡过程，换路后立即进入新的稳态。所以，灯泡会立即发亮，而且亮度不变化。

② 当开关闭合后，由于电感元件的储能特性，该支路存在过渡过程，换路时电感电流不能突变，换路后，电感电流逐渐增大，最后进入新的稳态，电流不变。所以，电感支路的灯泡开始由暗渐渐变亮，最后亮度不变。

③当开关闭合后，由于电容元件的储能特性，该支路存在过渡过程，换路时电容电压不能突变，换路后瞬时电容电压仍为零，电灯两边电压为US，电源通过电灯对电容充电，电容电压开始增大，电灯上的电流逐渐减小，直到电容电压等于US，进入新的稳态，电流为零。所以，电容支路的灯泡开始由亮渐渐变暗，最后熄灭。

由例3.5也可以得出过渡过程出现的条件是：

①电路中存在储能元件电容或电感。

② 电路发生换路。