电容器是一种能储存电荷的器件，电容元件是电容器的理想化模型。

电容元件的定义为：如果一个二端元件，在任一时刻t其存储的电荷q（t）与其两端电压u（t）之间的关系可以用u-q平面上的一条曲线来确定，则此二端元件称为电容元件，若该曲线为u-q平面上的一条过原点的直线，如图3-3所示，则此电容元件称为线性、非时变电容元件。本书讨论的仅指线性非时变电容元件。

当规定电容元件上电压的参考方向（极性）由正极板指向负极板时，则它的库伏关系为

电容元件的伏安特性

式（3.1）中C称为该元件的电容量，简称电容（capacitance）。C既表示电容元件储存电荷的能力，是一个与q、u无关的正实常数，也表示电容元件。在国际单位制中，电荷单位是库仑（C），电压单位为伏特（V），则电容单位为法拉（F）。电容的常用单位有微法（μF）和皮法（pF）。它们之间的换算关系为

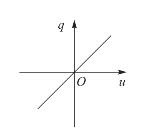
图3-3　电容元件的库伏特性

由式（3.1）可知，由于积聚在电容两极的电荷量与两极间的电压成正比，当加在极板两端的电压发生变化时，极板上的电荷量也随着改变，电荷量的改变必然要在电容电路中出现电流（实际电流并没有通过电容元件本身）。按图3-4所标电压电流的关联参考方向，可得电流

这就是电容元件的伏安关系（VAR）的微分形式。当时，电流的真实方向是流向电容的正极板，极板上的电荷增多，对电容充电；当时，电流的真实方向从正极板流出，极板上的电荷减少，电容放电。显然，电容在充放电过程中，就在电路中形成电流。

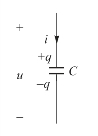
图3-4　电容元件的符号(www.daowen.com)

式（3.2）表明，通过电容的电流正比于电容上电压的变化率。当电容上电压变化时，才有电流，即只有电压在动态条件才有电流，所以电容元件又称动态元件。当电压不随时间变化时，即电压变化率为零，电容电流为零。故电容在直流情况下其两端电压恒定，这时电容电流为零，则电容相当于开路，所以称电容有隔断直流的作用。

式（3.2）还表明，如果任一时刻电容电流为有限值，则电容电压的变化率也必为有限值，这就意味着电容电压不能跃变，而只能是连续变化。如果电容电压发生跃变的话，那么电容电流就为无穷大值，即，显然这是不可能的，因为实际中电容上存储的电荷量不可能发生突然变化，因此，通过电容的电流总是为有限值，也就是说，电容电压的变化率为有限值，这是电容的一个重要性质。如果电容突然接入一个理想电压源，则是另一种情况在此暂不讨论。

和欧姆定律公式类似，如果电容的电压和电流的参考方向相反（非关联参考方向）则有

对式（3.2）两边同时积分，电容的伏安关系还可写成

上式中把积分变量t用ξ 表示，以区分积分上限t。式（3.4）称为电容元件伏安关系的积分形式。式（3.4）表明，某一时刻t电容电压u（t）取决于电容电流i（t）从-∞到t的积分，即与电容电流过去的全部历史有关，说明电容有“记忆”电流的作用，故电容是一种记忆元件。

将式（3.4）改写为

上式中t0为任意选定的初始时刻，u（t0）是t0时刻的电容电压值，称为初始电压。它是电容电流从-∞到t0时间的积分，反映了t0以前电容电流的全部历史。式（3.5）表明：如果已知t0时刻的初始电压u（t0）和电容电流i，就可以确定t≥t0时的电容电压u。

例3.1 图3-5（a）所示电路中，已知电容C＝1 F，电容电压u（t）的波形如图3-5（b）所示，试求电容电流i（t）的表达式。

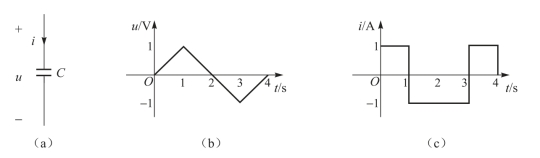
图3-5　例3.1图

解：先写出电容电压u（t）的表达式