最大功率传输定理

在电子电路中，常常遇到电阻负载如何从电路获得最大功率的问题。这类问题可以抽象为图2-49（a）所示电路模型来分析。二端网络N表示向电阻负载提供能量的有源线性电阻网络，它可以用戴维南等效电路来代替，如图2-49（b）所示。现讨论在什么条件下，负载能获得最大的功率？这就是最大传输定理要回答的问题。

根据图2-49（b）所示，负载电阻RL获得的功率为

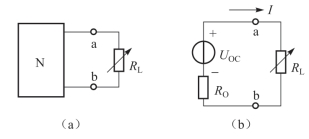
图2-49　最大功率传输定理

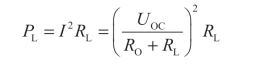
欲求PL的最大值，应满足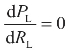，即

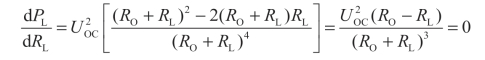
由上式求得RL获得最大功率的条件为

即负载从有源二端网络获得最大功率的条件是负载电阻等于二端网络的戴维南等效电路的电阻。这就是最大功率传输定理。当RL=RO时，称为最大功率匹配。在工程上，最大功率传输的条件也称为阻抗匹配。此时负载的最大功率为

(www.daowen.com)

若用诺顿等效电路，则

值得注意的是，式（2.48）所表达的负载RL获得最大功率的条件是在UOC、RO不变，RL可变的前提下推导出来的。如果不满足上述条件，则不能套用式（2.48）这一条件。

由以上结论可知，当满足最大功率匹配条件RL=RO时，RO吸收的功率与RL吸收的功率相等，对电压源UOC而言，功率传输效率为η=50%。但是，有源二端网络和它的等效电路，就其内部功率而言是不等效的，由等效电阻RO算得的功率一般并不等于网络内部消耗的功率。因此，实际上负载获得最大功率时，其功率传递效率不一定是50%。

在电子技术中，常常注重将微弱信号进行放大，而不注重效率的高低，因此常使用最大功率传输的条件，要求负载与电源之间实现阻抗匹配。例如扩音器的负载扬声器，应选择扬声器的电阻等于扩音器的电阻，使扬声器获得最大的功率。在电力系统中，输送功率很大，效率非常重要，要求尽可能提高电源的效率，以便充分地利用能源，故应使电源内阻（以及输电线路电阻）远小于负载电阻。

例2.19 电路如图2-50（a）所示，试求：（1）RL为何值时获得最大功率；（2）RL获得的最大功率；（3）电压源的功率传输效率。

解：断开图2-50（a）电路中负载RL，求点画线框中有源二端网络的戴维南等效电路的参数：

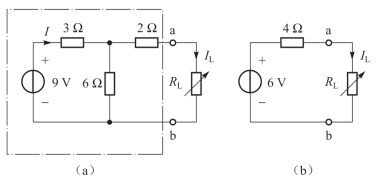
图2-50　例2.19电路图

如图2-50（b）所示，由此可知当RL=RO=4Ω时可获得最大功率。此时最大功率为