如要求图2-41(a)中RL以左的有源二端网络的等效电路,根据所学知识可采用以下方法:
①利用电源两种模型的等效变换进行化简,如图2-41(b)、(c)、(d)所示。最后化简成一个8 V电压源和一个8Ω电阻串联的模型,如图2-41(e)所示。
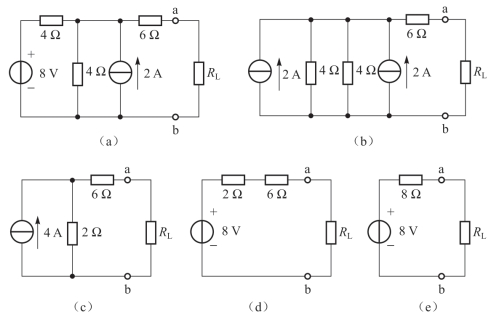
图2-41 有源二端网络的化简

戴维南定理
② 采用直接计算的方法:将RL断开,求出a、b端的开路电压UOC,如图2-42(a)所示。选取节点o为参考点,利用弥尔曼定理可得
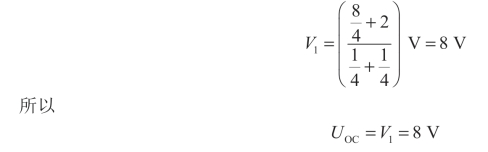
再求将所有电源置为零值时的两端等效电阻,如图2-42(b)所示。
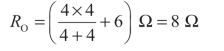
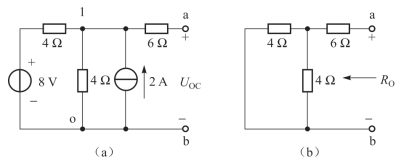
图2-42 开路电压及等效电阻
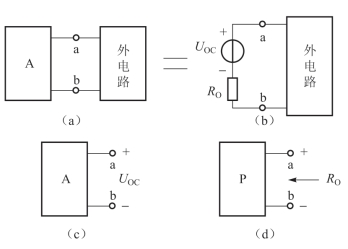
图2-43 戴维南定理
比较这两种方法,求出的开路电压UOC正好等于化简后的电压源的电压,求出的等效电阻RO正好等于电压源串联电阻的阻值。因此,在求一个有源二端网络的等效电路时,可以采用直接求解的方法。
将上述分析进行总结可得:一个线性有源二端电阻网络,对外电路来说,总可以用一个电压源和电阻串联的模型来代替。该电压源的电压等于有源二端网络的开路电压UOC,电阻等于该网络中所有电压源短路、电流源开路时的等效电阻RO,如图2-43所示。这就叫作戴维南定理。戴维南定理常用来分析电路中某一支路的电流或电压。
综上所述,归纳应用戴维南定理分析电路的步骤如下:
①将所求电流或电压的待求支路与电路的其他部分断开,得到一个有源二端网络。
② 求这个有源二端网络的开路电压UOC。
③将有源二端网络中的所有电压源用短路代替、电流源用开路代替,得到无源二端网络,求该无源二端网络的等效电阻RO。
④ 画出戴维南等效电路,并与待求支路相连,得到一个无分支闭合电路,再求所求电流或电压。
需要注意的是,画戴维南等效电路时,电压源的极性必须与开路电压的极性保持一致。此外,等效电路的参数UOC、RO除了用计算的方法外,还可采用实验的方法测得。
有源二端网络的开路电压UOC,可以用电压表直接测得,如图2-44(a)所示。等效电阻RO可以用电流表先测出短路电流ISC,如图2-44(b)所示,再计算出RO

戴维南等效电路参数的测量方法
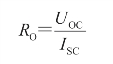 (https://www.daowen.com)
(https://www.daowen.com)
若二端网络不能短路,可串联一保护电阻R′,再测出电流![]() ,如图2-44(c)所示,此时有
,如图2-44(c)所示,此时有
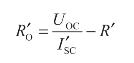
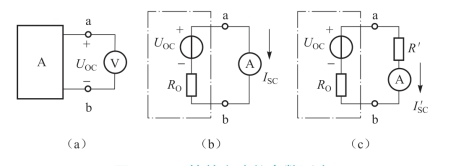
图2-44 等效电路的参数测定
例2.16 求图2-45(a)所示电路的戴维南等效电路。
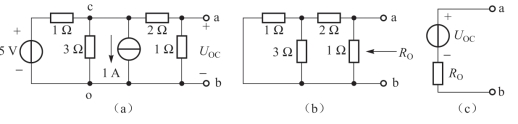
图2-45 例2.16电路图

戴维南定理的应用举例
解:先求有源二端网络的开路电压UOC。如图2-45(a)所示电路,选取节点o为参考点,利用弥尔曼定理可得
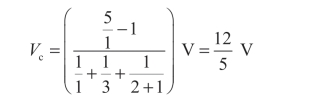
利用分压公式可得
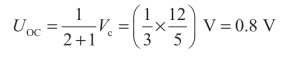
再求等效电阻RO,将有源二端网络转化成无源二端网络,如图2-45(b)所示电路,得
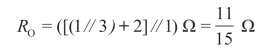
画出戴维南等效电路,如图2-45(c)所示电路其中
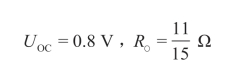
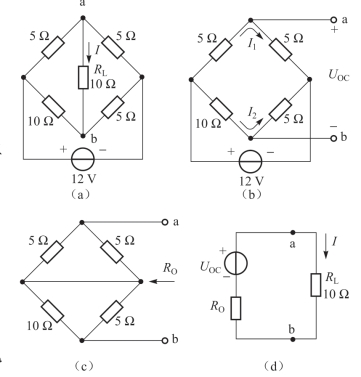
图2-46 例2.17电路图
例2.17 试用戴维南定理求图2-46(a)电路中流过RL的电流I。
解:将电阻RL移出,其余部分成为有源二端网络,如图2-46(b)所示,先求该图的开路电压UOC,可得
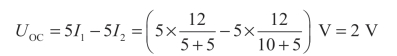
再求等效电阻RO,将有源二端网络转化成无源二端网络,如图2-46(c)所示电路,得
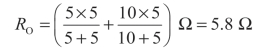
画出戴维南等效电路,并将移出的支路接入等效电路,如图2-46(d)所示,流过RL的电流为
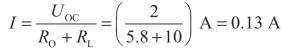
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。








