叠加定理（superposition theorem）是线性电路的一个重要定理。现以图2-32（a）所示电路为例来导出叠加定理的定义和应用。图中有两个独立电源，现求I，电流参考方向如图2-32所示。

叠加定理

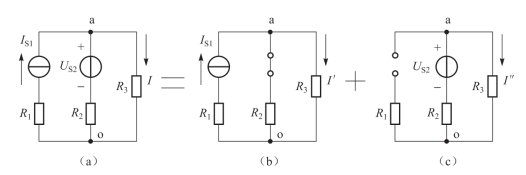
图2-32　叠加定理举例

对图2-32（a），选取节点o为参考点，根据弥尔曼定理可求得节点a的电位为

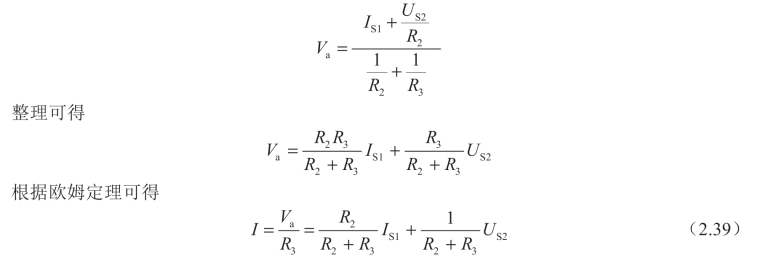
从式（2.39）可看出，通过R1的电流由两部分组成。第一部分仅与IS1、R2、R3有关，可看成只有IS1单独作用时，通过电阻R3的电流，此时US2不起作用，即US2=0，用短路线代替，如图2-32（b）所示。由图2-32（b）可知，此时流过R3的电流为

正好与式（2.39）中第一项相符。第二部分仅与US2、R2、R3有关，可看成只有US2单独作用时，通过电阻R3的电流，此时IS1不作用，即IS1=0，用开路代替，如图2-32（c）所示。由图2-32（c）可知，此时流过R3的电流为

正好与式（2.39）第二项相符。从上述分析可得：

这一特性被称为叠加定理。

将上述结论推广到一般线性电路，叠加定理可表述为：当线性电路中有几个独立电源共同作用时，各支路的电流（或电压）等于各个独立电源单独作用时在该支路产生的电流（或电压）的代数和（叠加）。

叠加定理在线性电路的分析中起着重要作用，它是分析线性电路的基础。线性电路的许多定理可以从叠加定理导出。在运用叠加定理时，也可以把电路中所有的电压源和电流源分成几组，按组计算电流和电压后再叠加。

使用叠加定理时，应注意以下几点：

①叠加定理只能用来计算线性电路的电流和电压，对非线性电路叠加定理不适用。由于功率不是电压或电流的一次函数，所以也不能应用叠加定理来计算。

② 叠加时，电路的连接及所有电阻保持不变。不作用的电压源用短路线代替；不作用的电流源用开路代替。

③所求响应分量叠加时，若分量的参考方向与原电路中该响应的参考方向一致，则该分量取正号，反之取负号。

例2.12 如图2-33（a）所示电路，已知IS1=10 A，US2=10 V，R1=2 Ω，R2=1 Ω，R3=5 Ω，R4=4 Ω，试用叠加定理计算I和US1。(www.daowen.com)

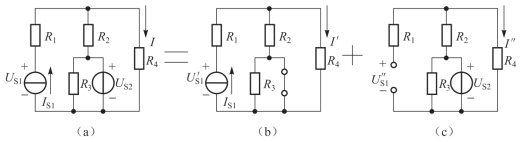
图2-33　例2.12电路图

叠加定理的应用举例

解：按叠加定理，作出电流源和电压源分别作用的分电路，如图2-33（b）和（c）所示。

①电流源单独作用时，由分流公式可得

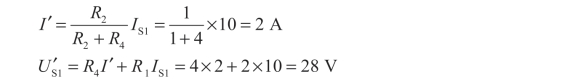
② 电压源单独作用，由欧姆定律可得

③将单独作用的分量进行叠加

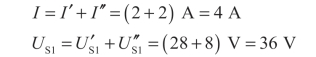
例2.13 如图2-34（a）所示电路，已知IS=3 A，US=20 V，R1=20 Ω，R2=10 Ω，R3=30 Ω，R4=10 Ω，试用叠加定理计算U。

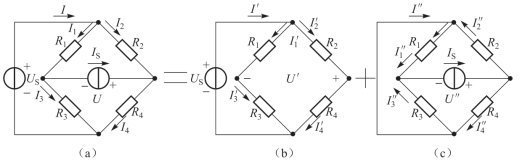
图2-34　例2.13电路图

解：按叠加定理，作出电压源和电流源分别作用的分电路，如图2-34（b）和（c）所示。

①电压源单独作用：

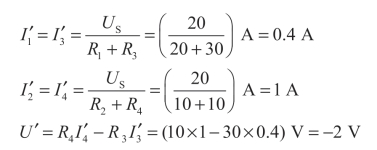
② 电流源单独作用：

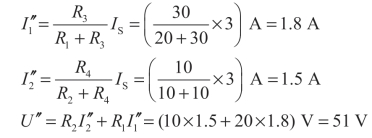
③将单独作用的分量进行叠加：