前几节中介绍的分析电路的方法是利用等效变换，将电路化简成单回路电路后求出待定支路的电流或电压。但是对于复杂电路（例如多回路多节点电路）往往不能很方便地化简为单回路电路，也不能用简单的串、并联方法计算其等效电阻，因此需考虑采用其他分析电路的方法。本节介绍其中最基本、最直观的一种方法——支路电流法（branch current method）。

支路电流法是以各支路电流为未知量，利用各元件上的VAR、电路中各节点的KCL和回路的KVL约束关系，列出数目足够且相互独立的方程组，求解出各支路电流，然后根据电路的基本关系求出其他未知量。下面以图2-23为例来说明支路电流法的分析过程。

设图2-23中各电压源电压和电阻阻值均已知，求各支路电流。从图中可看出支路数b=3，节点数n=2，各支路电流的参考方向如图所示。未知量为三个，因此需列出三个方程来求解。

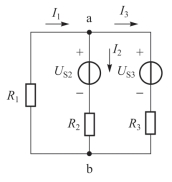
图2-23　支路电流法举例

首先，根据电流的参考方向对节点列KCL方程：

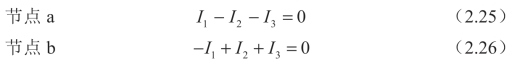
可以看出，式（2.25）、式（2.26）完全相同，故只有一个方程是独立的。这一结果可以推广到一般电路：具有n个节点的电路，只能列出n-1个独立的KCL方程。所以，n个节点中，只有n-1个节点是独立的，称为独立节点。

其次，对回路列KVL方程，图2-23中有三个回路，绕行方向均选择顺时针方向。

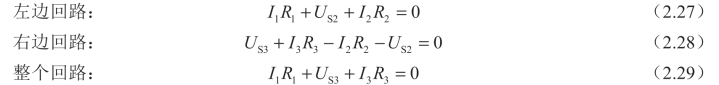
将式（2.27）与式（2.28）相加正好得到式（2.29），可见在这三个回路方程中独立的方程为任意两个，这个数目正好与网孔个数相等。由此可以推论：若电路有n个节点，b条支路，m个网孔，可列出［b-（n-1）］个独立的KVL方程，且［b-（n-1）］=m。通常情况下，可选取网孔作为回路列KVL方程，因为每个网孔都是一个独立回路（包含一条在已选回路中未出现过的新支路），对独立回路列KVL方程能保证方程的独立性。值得注意的是，网孔是独立回路，但独立回路不一定是网孔。

通过以上实例可得出，以支路电流为未知量的线性电路，应用KCL和KVL一共可列出（n-1） +［b-（n-1）］=b个独立方程，可以解出b个支路电流。

综上所述，归纳支路电流法的计算步骤如下：

①选定各支路电流的参考方向。

② 选择（n-1）个独立节点列KCL方程。

③选取［b-（n-1）］个独立回路，设定各独立回路的绕行方向，对其列KVL方程。(www.daowen.com)

④ 联立求解上述b个独立方程，得出待求的各支路电流。

例2.6 在图2-23电路中，已知R1=6 Ω，R2=R3=5 Ω，US2=80 V，US3=90 V，试求各支路电流。

解：设各支路电流的参考方向如图2-23所示，并指定网孔的绕行方向为顺时针方向，应用KCL和KVL列出式（2.25）、式（2.27）及式（2.28）的方程组，并将数据代入，可得

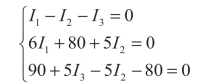
解得

计算得出的结果可以采用以下两种方法进行验算：

①将计算结果代入求解时未用过的回路方程中，得

表明计算正确。

② 利用电路中功率平衡关系进行验算：

电源的功率为US2I2+US3I3=[80×（-4）+90×（-6）] W=-860W＜0W 即产生功率860W。

电阻上的功率为

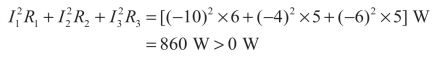
即吸收功率860 W。

吸收的功率等于产生的功率，即功率平衡，表明计算正确。