
1.电阻的串联
两个或两个以上电阻首尾相连,中间没有分支,各电阻流过同一电流的连接方式,称为电阻的串联(series connection)。图2-4(a)为三个电阻串联电路,a、b两端外加电压U,各电阻流过电流I,参考方向如图所示。
由图2-4(a)所示,根据KVL和欧姆定律,可得
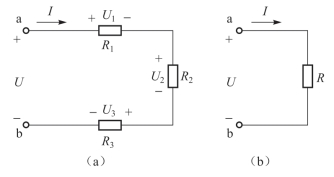
图2-4 电阻的串联
![]()
由图2-4(b)所示,根据欧姆定律,可得
![]()
两个电路等效的条件是具有完全相同的伏安特性,即式(2.1)与式(2.2)完全一致,由此可得
![]()
式(2.3)中R称为串联等效电阻,式(2.3)表明串联电阻的等效电阻等于各电阻之和。推广到一般情况:n个电阻串联等效电阻等于各个电阻之和。即

电阻串联时电流相等,各电阻上的电压为
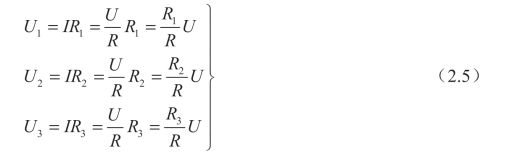
写成一般形式

式(2.6)为串联电阻的分压公式。
由此可见,电阻串联时,各个电阻上的电压与电阻值成正比,即电阻值越大,分得的电压越大。同理,电阻串联时每个电阻的功率也与电阻值成正比。
2.电阻的并联
两个或两个以上电阻的首尾两端分别连接在两个节点上,每个电阻两端的电压都相同的连接方式,称为电阻的并联(parallel connection)。图2-5(a)为三个电阻并联电路,a、b两端外加电压U,总电流为I,各支路电流分别为I1、I2和I3,参考方向如图中所示。
对图2-5(a),根据KCL和欧姆定律,可得
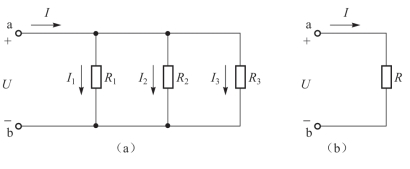
图2-5 电阻的并联
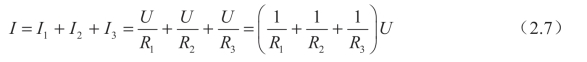
对图2-5(b),根据欧姆定律,有

两个电路等效的条件是具有完全相同的伏安特性,即式(2.7)与式(2.8)完全一致,由此可得

或
![]() (www.daowen.com)
(www.daowen.com)
式(2.9)中R称为并联等效电阻;式(2.10)中G1、G2、G3为各电阻的电导,G称为并联等效电导。
推广到一般情况:n个电阻并联,其等效电阻的倒数等于各个电阻的倒数之和。即n个电阻并联的等效电导等于各个电导之和。即

电阻并联等效时,计算等效电阻的表示式常用R=R1//R2//R3…表示。电阻并联时电压相等,各电阻上的电流为
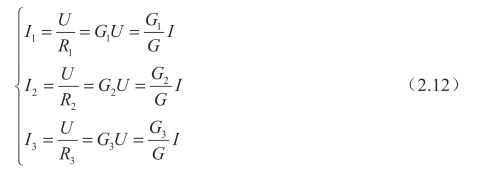
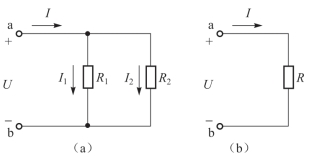
图2-6 两个电阻的并联
式(2.12)为并联电阻的分流公式。
由式(2.12)可见,电阻并联时,各个电阻上的电流与电阻值成反比,即电阻值越大,分得的电流越小。同理,电阻并联时每个电阻的功率也与电阻值成反比。
常遇到两个电阻并联的情况,如图2-6(a)所示,其等效电阻[见图2-6(b)]为

利用分流公式(2.12)得各支路电流为

在应用分流公式时,要注意各支路电流与总电流的参考方向是否一致。
3.电阻的混联
电阻的连接既有串联又有并联时,称为电阻的混联。这种电路在实际工作中应用广泛,形式多种多样。
在分析这样的电路时,往往先求出混联电路二端网络的等效电阻,然后利用定律和公式求出其他量。那么,关键就是求等效电阻,即判断出哪些电阻串联,哪些电阻并联。对于较简单的电路可以通过观察直接得出,如图2-7所示的混联电路中,可以直接看出R1~R4串并联关系,故可求出a、b两端的等效电阻Rab为
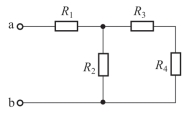
图2-7 电阻的混联
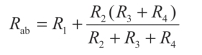
当电阻串、并联关系不能直观地看出时,可以在不改变元件间连接关系的条件下将电路画成比较容易判断串、并联关系的直观图。下面通过例2.1来说明。
例2.1 求图2-8(a)所示电路a、b两端的等效电阻。
解:对于这样的电路,可以按如下步骤分析:
①将电路中有分支的连接点依次用字母或数字编号并排序,如图2-8(a)中a、c、c′、d、b。将无电阻导线(即短路线)两端的点c、c′合并为同一点c(c′)。
② 依次把电路元件画在各点之间,得到直观图,如图2-8(b)所示。
③根据直观图,利用串、并联等效电阻公式求出其等效电阻。
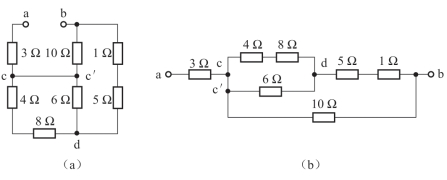
图2-8 例2.1电路图
根据图2-8(b)可直观地看出等效电阻为
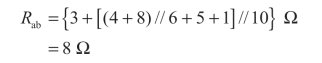
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






