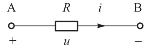
图1-13　电阻

电阻元件作为一种理想电路元件，在电路图中的图形符号如图1-13所示。电阻的大小与材料有关，而与电压、电流无关。若给电阻通以电流i，这时电阻两端会产生一定的电压u，电压u与电流i的比值为一个常数，这个常数就是电阻R，即，这也就是物理中介绍过的欧姆定律（Ohm’s Law），其表达式可表示为

值得说明的是，式（1.12）是在电压u与电流i为关联参考方向下成立的。若u、i为非关联参考方向，则欧姆定律表示为

当然，欧姆定律也可以表示为

式（1.12）～式（1.15）反映了电阻元件本身所具有的规律，也就是电阻元件对其电压、电流的约束关系，即伏安关系（VAR）。

根据电阻值R的大小，在电路中有两种特殊工作状态：

①当R=0时，根据欧姆定律u=Ri，无论电流i为何有限值，电压u都恒等于零，我们把电阻的这种工作状态称为短路。

② 当R=∞时，根据欧姆定律无论电压u为何有限值，电流i都恒等于零，我们把电阻的这种工作状态称为开路。

如果把电阻元件上的电压取作横坐标，电流取作纵坐标，画出电压与电流的关系曲线，则这条曲线称为该电阻元件的伏安特性曲线，如图1-14所示。

(www.daowen.com)

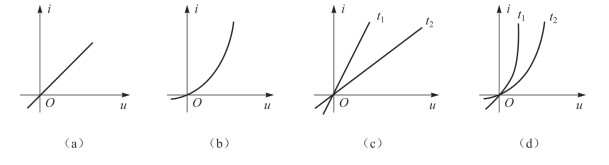
图1-14　电阻元件的伏安特性曲线

若电阻元件的伏安特性曲线不随时间变化，则该元件为时不变电阻，如图1-14中的图（a）和图（b）；否则为时变电阻，如图1-14中的图（c）和图（d）。若电阻元件的伏安特性曲线为一条经过原点的直线，则称其为线性电阻，如图1-14中的图（a）和图（c）；否则为非线性电阻，如图1-14中的图（b）和图（d）。

所以，图1-14中，图（a）为线性时不变电阻，图（b）为非线性时不变电阻，图（c）为线性时变电阻，图（d）为非线性时变电阻。

因而，广义的电阻元件定义如下，在任一时刻t，一个二端元件的电压u和电流i两者之间的关系可由u- i平面上的一条曲线确定，则此二端元件称为电阻元件。

严格地说，电阻器、白炽灯、电烙铁、电加热器等实际电路元件的电阻或多或少都是非线性的。但在一定范围内，它们的电阻值基本不变，若当作线性电阻来处理，是可以得到满足实际需要的结果。线性电阻在实际电路中应用最为广泛，本书将主要讨论线性元件及含线性元件的电路，以后如果不加特别说明，本书中的电阻元件皆指线性电阻元件。

为了叙述方便，常将线性电阻元件简称电阻。这样，“电阻”及其相应的符号R一方面表示一个电阻元件，另一方面也表示这个元件的参数。

例1.4 如图1-15所示，已知R=100 kΩ，u=50 V，求电流i和i'，并标出电压u及电流i、i'的实际方向。

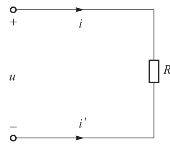
图1-15　例1.4图

解：因为电压u和电流i为关联参考方向，所以

而电压u和电流i'为非关联参考方向，所以

电压u＞0，表示其实际方向与参考方向相同；电流i＞0，表示其实际方向与参考方向相同；电流i'＜0，表示其实际方向与参考方向相反。从图1-15中可以看出，电流i和i'的实际方向相同，这说明电流实际方向是客观存在的，与参考方向的选取无关。