对于再淹没过程，最关心的是骤冷前沿上升的速度。计算模型可分成两类，一类是根据再湿前沿附近实际存在的传热和流动工况求解再淹没过程，现代大型计算机程序使用这种方法。另一类是所谓的“导热再湿模型”，认为壁面再湿润是由再湿前沿附近包壳的轴向导热决定的。下面我们介绍这种方法。

图6-27表示包壳表面再湿前沿附近的传热工况。假设：①包壳的壁厚δ和物性为常数，包壳无限长；②燃料的热导率比包壳低得多，因而可以把燃料与包壳的交界面看作是绝热的；③包壳无内热源；④冷却剂的温度为常数且等于饱和温度。上述假设意味着在包壳内进行的是一维导热过程，其导热方程为：

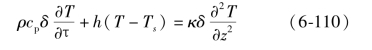
式中 h——再湿前沿处湿区换热系数。

设再湿前沿以不变速度V向前推进。为求解方便，引进一个新的坐标ζ=z-Vτ。该坐标以再湿前沿为原点，并跟随再湿前沿一起移动。由于

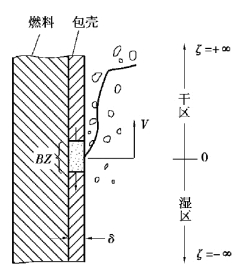
图6-27　导热再湿模型

方程（6-110）可以写成

式（6-113）建立了速度V与轴向导热过程的联系。湿区（ζ≤0）换热系数h等于常数，干区（ζ>0）的换热系数等于零，且方程的边界条件为

式中 T0——再湿温度，即壁面可被水浸润时的温度；

Tco——上游壁面初始温度；

Ts——饱和温度。(www.daowen.com)

这样，方程（6-113）在湿区的解为

利用包壳传给水的热量是靠自身温度的降低来补偿的热平衡的概念，即

将方程（6-114）代入式（6-115）左侧，积分可得

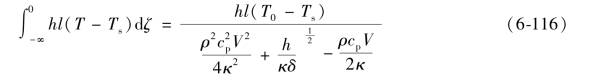
式中 l——包壳周界长度。

将式（6-115）和式（6-116）联立，可以得到再湿前沿移动速度的计算式：

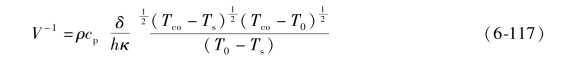
如果初始壁温很高，致使（Tco-Ts）≫（T0-Ts），面积（Tco-Ts）≈（Tco-T0），这时式（6-117）可以简化为

式（6-118）表明，再湿前沿移动速度的倒数近似与包壳再湿温度之间的壁温初始值呈线性关系，这已为实验所证实。但式（6-117）中却隐藏着一个不合理的成分，即在用该式拟合实验数据时，导出的换热系数为106 W/（m2·℃）的量级，这样大的换热系数是难以想象的。为了得到更合理的解，需要考虑使用二维模型，并对换热工况做出更合理的假设。

在讨论上述解法时，都是将再湿温度T0当作已知参数。但是准确地确定这个温度非常困难。这主要是因为表面骤冷是一种很快的瞬态过程，再湿温度很难测准。而且这一温度似乎还与固体表面的状况，例如是否有氧化膜等因素有关。目前还没有公认的再湿温度数据。在整理实验数据时，每位学者选用的再湿温度都是不同的。但是他们根据再湿温度T0与骤冷前沿处的换热系数h（z）总是在模拟中同时出现的特点，配套选用它们的数值，即可得到很好的模拟效果，可以回避选择再湿温度是否准确的问题。图6-28给出了一组再湿温度的实验数据。根据这些数据可以看出，压力在4 MPa以下时，再湿温度大约比饱和温度高100℃，而在4 MPa以上的压力下，数据很分散，但总的趋势是压力越高，再湿温度与饱和温度的差值越小，有时甚至高出饱和温度只有20℃左右。

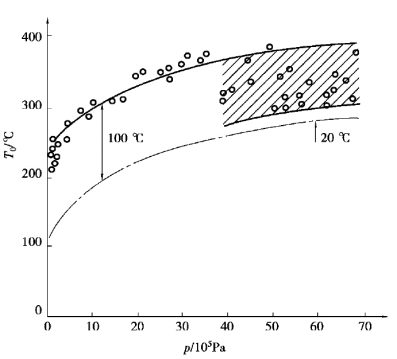
图6-28　再湿温度与压力的关系