假定入口流速有如下特性：

与前面提到的恒定入口焓和轴向加热功率q′的假设一致。首先在图6-13中为不同的时间域t<v和t>v分别定义适当的λ（t）。

根据ρl=ρf的假设，对于最初不在通道中的流体（将在t>v时到达两相区），由式（6-56）得

对于最初在通道内，但在t<v时达到两相点的单相流体，有

因此

表6-3总结了适用于两个时间域的λ（t）值，以及它们在时间-空间域（ⅠA、ⅠB、ⅠC、ⅡA和ⅡB）的重要特征。

现在来定义它们的时间—空间关系。对于两相区，我们必须分别考虑区域Ⅰ和区域Ⅱ。区域Ⅰ是在t>0时进入两相区的区域。

表6-3　通道各种两相区域的沸腾边界

对于区域Ⅰ：为了获得干度值，在条件x=0，t=tB下对式（6-67）积分，则有

因此，需要参数tB来得到干度值。它是通过对式积分得到的，对于常数Ω和假定的流量指数衰减，有

为了获得参数tB，使用tB中λ（t）的适当值和适当的初始条件对式（6-76）积分。3个分区域的结果是：

对于分区域ⅠA：t>tB>v；使用λ（tB>v）和t=tB，z=λ（tB）时的初始条件得到

对于分区域ⅠB：v>t>tB；使用λ（tB<t）和在t=tB，z=λ（tB）处的初始条件得到

对于分区域ⅠC：t>v>tB；使用λ（tB>v）和在t=v，z=zⅠB处的初始条件（因为当t=v时，流体域从ⅠB穿越到ⅠC），得到

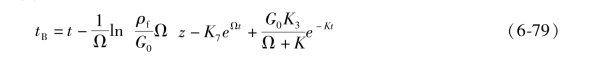
注意对于任意的z和t的组合，式（6-77）—式（6-79）可以用来确定tB。常数Ki定义为

对于区域Ⅱ：这是在t≤0时处于两相状态的区域。当t=0时，在条件x=x0和z=z0下，对式（6-67）积分得到(www.daowen.com)

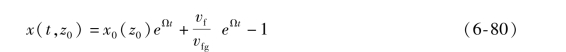
x0的值由稳态能量平衡确定：

注意式（6-76）可以使用表6-3中适当的λ值进行积分得到两个分区域。对于区域ⅡA（t<v），在t=0，z=z0时，有

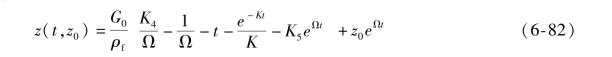
对于区域ⅡB（t>v），在t=v，z=zⅡA时，有

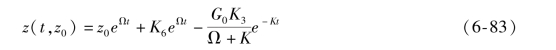
其中，

表6-3和表6-4总结了关于这一问题的解和每个区域的重要特征。

表6-4　通道内两相区沸腾干度和时间的表达式

【例6-3】 流量减少所致沸腾起始的时间

问题：假设液体通过加热管轴向流动。当t=0时，入口流量开始呈指数下降：

式中，t的单位为s，假设入口的初始流速Vin（0）=3.05 m/s。试确定通道中沸腾开始的时间。忽略壁面摩擦和液体压缩性，假设入口温度和加热功率保持不变。

已知信息：管道直径d=12.7 mm；管道加热长度L=3.05 m；加热线功率密度q′=16.4 kW/m；入口水温Tin=204℃；水在6.9 MPa下，ρf=740 kg/m3；cp=4.2 kJ/kg·K；Tsat=285℃；假设ρl=ρf=740 kg/m3。

解 先获得通道出口处的冷却剂焓达到沸腾所需的时间。

利用特征线法，因为流体最初在通道中加热，首先假设t值小于v。

将式（6-56）在t<v内积分，得到式（6-74），用Vin（0）代替G0/ρf，并将K设为单位1：

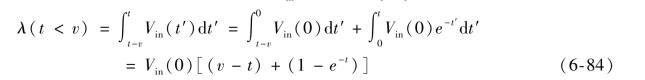
利用式（6.60），有：

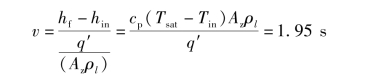
因为沸腾最初发生在出口处，设λ（t<v）=L=3.05 m，可以从式（6-84）得到t。注意，如果发现时间t为负时，则t<v的假设不正确，并且必须获得t>v时的λ值。

求解式（6-84），得到t的结果：