特征线法已应用于各种两相流模型。Tong和Weisman考虑了具有相同速度和处于热平衡的汽液均相流模型。Gidaspow和Shin引入了两流体模型，该模型对两相相对速度有特定本构方程。他们的模型产生了一组具有所有真实特征的“适定”方程组。根据本构关系，两流体模型可能是“病态”的，在这种情况下，一些特征变为假想的，导致数值解不稳定性。

为了说明在两相流问题中的应用，我们将在恒定系统压力和热平衡的均匀流的假设下，考虑沸腾通道。而通道的单相区域可以用6.2.1节中给出的方式来处理。

让我们首先定义单相区和两相区之间的边界。该边界将由两个参数表征：

λ（t）——流体达到饱和状态时沿通道的距离。此距离如图6-11所示。

v——流体进入流道后失掉其过冷度所需要的时间。

在假设中，假定单相区的质量流量是恒定的，Gm（z，t）=Gin（t）。对于恒密度的液体，有：

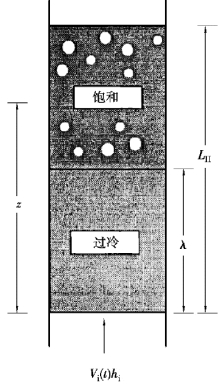
图6-11　受热通道内的基本区域

因此，参数λ（t）可以通过对dz/Gm=dt/ρm的积分得到：

对于恒定的系统压力，就像6.1节的MI模型那样，能量方程（6-31）可以写成

根据式（6-43），从式（6-57）得到特征方程：

其中，q′=q″Ph。

如果沿通道的热流密度在轴向和时间上是常数，则可以很容易地在入口焓和饱和焓之间对式（6-58）积分：

或

因此，v是流体包进入通道后失去过冷度所需时间。需注意的是，由于体积加热（q′/Az）是恒定的，如果入口焓也是恒定的，则v也是恒定的。然而，流动距离λ（t）随速度而变化，如式（6-56）所示。对于进口流量减小的瞬态过程，λ（t）的位置如图6-12所示。注意，因为入口焓和轴向热量输入保持恒定，因此v也是恒定的。

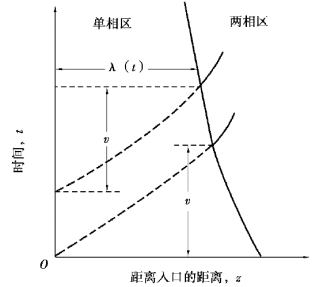
图6-12　入口流量减小通道的主要特性（单相区）

现在把注意力转向两相区域（即z>λ）。在该区域中，连续性方程（6.1）可以写为：

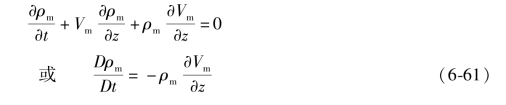
混合物的密度和焓可写为：

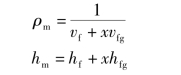(www.daowen.com)

式中 x——两相混合物的干度。

我们可以明确地将速度变化与干度和各相比体积联系起来：

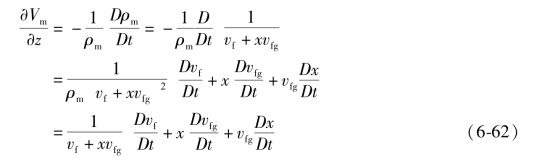
在这里所应用的条件，液相为不可压缩流体（Dvf/Dt=0）和近恒定系统压力（D vfg/Dt=0），因此有：

对其积分，得到：

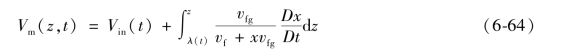
能量方程可用于确定流动干度。根据式（6-58），在恒定系统压力下（hfg和hf恒定），得到

定义特征沸腾频率参数Ω为

则式（6-65）简化为

结合式（6-64）和式（6-67），干度变化率可以消掉，因此有

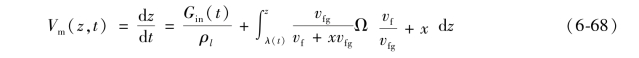
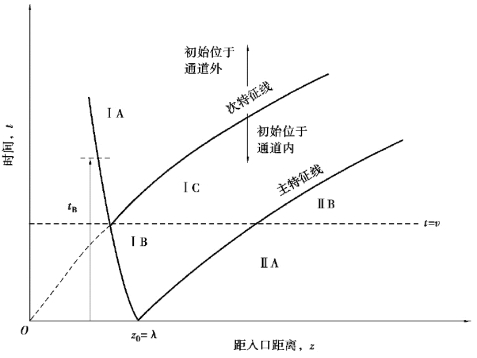
图6-13　两相区流体流量减小或热输入量增加的通道主要特性

或

式（6-67）是干度随时间变化所需要的一般关系式，式（6-69）是位置随时间变化的一般关系式。需要注意的是，入口的ρl值几乎等于饱和值ρf，因此在实际应用中，一般将ρl视为ρf。

有两个流体域需要考虑：即最初在两相区外的流体域和最初在两相区内的流体域。最初在饱和区的液体定义了主特征线，如图6-13所示。

考虑到最初出现在两相区（图6-13中的区域Ⅱ）中的流体，初始条件定义为

最初在两相区之外的流体，包括那些在流道之外的流体（图6-13中的区域Ⅰ），在时间tB到达两相区。在时间tB，流体开始发生沸腾的x和z的条件是

在这些假设下，Ω是一个常数，因此对于所有具有实际意义的Gin（t），式（6-67）和式（6-69）等两个方程都是可积的。因此，对于任何定压流量瞬态过程，我们可以得到作为时间和空间的函数的流体速度和干度随加热长度变化的精确解。下面将通过在通道中的流量指数衰减的例子来说明这个问题。