在流体系统中，特征线定义了z-t空间中如流体团或在流体中传播的扰动等的传播路径。如果考虑一维管道内的流动，则将其特征线定义在二维空间中，扰动的轴向作为一维，时间作为另一维。需要注意的是，这些特征线与特定物理系统中的传播能力有关，而不是与特定传播过程有关。即使不存在物理干扰，也可以定义它们。

使用Tong和Weisman所讨论的问题可以很容易说明MOC方法。考虑单个加热通道的流动瞬态过程中的行为。假设入口质量流速遵循式（6-45）：

式中，当t>0时，G0是常数。此外，假设系统在t=0时为稳态，在整个瞬态过程中，热流密度q″（z）和入口焓hin保持其稳态值不变。如果系统压力恒定，即与z和t无关，则冷却剂焓hm的变化为[与热膨胀流体的式（6.18）相同]：

式中 Ph——单位长度的壁面面积。

设ρm为常数，因为Gm（z，t）等于Gin（t），则方程变成了6.1.3节的SV模型。式（6-46）就有了与式（6-4）相同的形式，因此特征方程变为

注意，即使ρm依赖于hm，式（6-47）仍然有效。

式（6-47）有两个解。一个解属于瞬态开始时在反应堆内给定位置z0存在的流体域。流体质点的后续位置由图6-10中区域Ⅰ适当的线表示。第二个解属于在瞬态开始时尚未进入反应堆的第二个流体域。这部分流体可以用t0来描述，表示从瞬态开始到这部分流体进入反应堆时的时间间隔。该部分流体的位置时间特性由图6-10的区域Ⅱ内的线表示。区域Ⅰ和区域Ⅱ通过特性极限分开，特性极限对应于瞬态开始时刚好处于反应堆入口的流体，即z0=0和t0=0。

图6-10　假想流动瞬态中时间-距离关系

通过积分dz/Gm=dt/ρm来确定区域Ⅰ的解，得到

它描述了区域Ⅰ的特征线方程，表示了流体的路径。对积分，得到(www.daowen.com)

式中，h0（z0）是零时间和轴向位置为z0处冷却剂的焓，而G0则是t=t0时的质量流速。根据稳态条件得到h0（z0），并将其代入式（6-49），得到

式中 hin——入口焓。

用式（6-48）求解得到（1+t）后，将其代入式（6.50），最后得到：

对于给定的热流密度分布，对式（6-51）积分，获得从z0开始的任何流体包在z处的焓。相应的时间由式（6-48）得到。

为了得到区域Ⅱ的解，对dz/Gm=dt/ρm积分，现在从流体首次进入反应堆的时间开始（在z=0的时间）到t进行积分，得到：

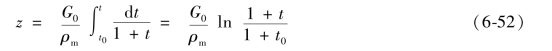
该方程描述了图6-10中区域Ⅱ的特性曲线。对从0到z积分，并代入（1+t）的关系，得到

特性极限曲线是在z0=0的区域Ⅰ内式（6-52）的解，也是t0=0时区域Ⅱ内式的解。因此有

上述例子的解是完整的，因为流体的焓和流速在每个空间和时间点都是已知的。在区域Ⅰ中，hm（z，t）由式（6-51）和式（6-48）给出，而在区域Ⅱ，则由式（6-53）和式（6-52）给出。根据定密度的假设，在任何给定时间，通道中任何地方的流速都相等，即V（z，t）=Vin（t）。对于流速远小于声波速度的液体，该模型是合理的。然而，在许多情况下，评估伴随局部流体速度突变的压力扰动很重要。这时，分析中应同时考虑连续性方程和动量守恒方程。