作为单质量流速模型的一种简化，可以在通道长度上对质量和能量方程积分。因此，质量守恒变为

式中 M——单位面积全长通道内混合物的总质量。

能量方程的微分守恒方程为

对其积分得到

注意根据式（6-27），可以写出

其中，hin=hm（z=0），hout=hm（z=L），设hin为常数。因此，将式（6-31）代入式（6-30），得到：

其中

为了对式（6-33）进行积分，需要有焓的轴向分布。可以用式（6-35）定义形状因子β（z）

其中，hm（0，t）为常数，等于hm（0，0），为整个流道的平均焓。

所定义的形状因子β（z）满足如下关系

在实际工程中，β（z）通常用稳态解来代表。

此外，可以假设质量流速的分布与流体热膨胀有关，如

其中，

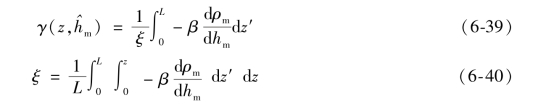
因此，在通道积分模型中，求解质量方程（6-27）、动量方程（4-99）和能量方程（6-32），得到M、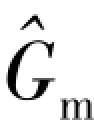和E的值，而式（6-35）和式（6-38）分别给出了hm（z，t）和Gm（z，t）的局部值。

这个方法是一个比单质量速度模型更可接受的近似动量积分模型，特别是在快速沸腾的情况下。然而，由于焓分布需要预先设定，如果对通道中的焓输运的动态过程和分布特别感兴趣，则应避免采用这种近似。上面讨论的各个近似模型在表6-1中给出了它们的一些特性。

表6-1　各动量方程近似解模型的特性

【例6-1】 压水堆入口压力瞬态

问题描述：考虑压水堆通道入口处压力突然降低，其出口压力保持恒定：

式中 t——时间，s。

堆芯几何和运行条件见表6-2。

表6-2　例6-1表

续表

注：瞬态条件：
a.压力下降瞬态：pin（t）-pout=0.5　pin（0）-pout （1+e-400t），t为时间，s；
b.热流密度上升瞬态：q′（t）=1.1q′（0）。(www.daowen.com)

解 分别采用上述4种模型求解，并将结果进行比较。在这些计算中，通道被分成10个轴向段（节点）。Lee和Kazimi给出了关于问题有限差分格式的详细信息。

A.流道内流动的短期响应。

a.分段可压缩（SC）模型：图6-1。在入口位置，由于压力降低，质量流速开始减小，随着时间的推移，这种扰动传播到通道中。计算得到的声速约为900 m/s，该声波的通道穿过时间约为4.1 ms。当t<4.1 ms时，质量流速的快速下降的影响尚未到达通道的末端，即下游区域尚未受到压力波的影响。图6-1显示因为有限差分分段的影响，当t<4.1 ms时，G（L，t）减少。

图6-1　采用SC模型时入口压力瞬态下压水堆的短期响应

当t>4.1 ms时，反射压力波对质量通量分布的影响很短。由于恒定出口压力的假设，入射膨胀波将在出口边界处被压缩为压缩波。因此，波的传播方向相反，振幅相同，但符号相反。在t=5 ms时的分布和此时间之后的分布反映了反射波从通道出口向入口传播的效应。净质量流量是前向波和反射波叠加的结果。

在此短期时间内，平均质量流速比仅从1.00下降到0.98。

b.动量积分（MI）模型：图6-2。无限声速传播的假设导致因压力扰动而致局部质量流速变化的动态特性完全损失。只看到平均质量流速下降的趋势。

图6-2　采用MI模型时入口压力瞬态下压水堆的短期响应

有两个原因导致了平均质量流速和稳态曲线斜率的变化：

i.入口压力的降低使驱动力降低，从而降低了通道的平均质量流速。

ii.由加热所致的流体膨胀使流量小斜率升高，即Gin小于Gout。

c.通道积分（CI）模型：图6-3。瞬态开始后，质量流速曲线出现突变。原因是Cl模型应用了基于稳态焓分布的质量、动量和能量的全局平衡。由于在入口附近的Gm减小，hm增大，这使得在通道末端两相流膨胀。

图6-3　采用CI模型时入口压力瞬态下压水堆的短期响应

CI模型预测的Gm分布与MI模型预测的结果在t≥3 ms时的Gm特性吻合较好，证明瞬态焓分布与稳态焓分布没有太大的差异。因此可以认为，对单相（液体）流的瞬态过程，CI模型是MI模型的一个很好的近似。

d.单质量流速（SV）模型：图6-4。采用刚体近似，速度在整个通道内保持恒定。

SV模型预测的质量流速与MI模型和CI模型预测的平均质量流速几乎相同，这是对液相流动瞬态过程的一个所期望的结果。

图6-4　采用SV模型时入口压力瞬态下压水堆的短期响应

图6-5　压水堆入口压力瞬态的入口质量流速变化过程

B.流道流动的长期响应。图6-5示出了用MI、CI和SV等模型预测的入口质量流速的变化过程。即使在沸腾开始后（t=1.1 s），3种模型预测的出口质量流速仍然很接近。

MI模型的长期响应实质上是短期响应的延续。随着流体热膨胀，平均质量流速保持了的趋势，并且随着接近新的稳态条件，稳定下降，最终稳定在一个较小的质量流速下。在整个瞬态过程中，CI模型的计算结果与MI模型吻合得很好。这表明，除非发生显著沸腾，CI模型能对压水堆的瞬态过程进行良好的预测。即便显著低估了出口附近的沸腾量，SV模型也显示出与前两个模型吻合较好。

图6-6和图6-7显示了SC和MI模型的Gm分布，其质量流速在轴向逐渐增大。很明显，由于沸腾的原因，在最后一个节点中MI模型的热膨胀提高了出口流量，但增加的幅度比用SC模型计算的结果要小。

图6-6　采用SC模型计算的压水堆入口压力瞬态时的流量分布

图6-7　采用MI模型计算的压水堆入口压力瞬态时的流量分布

【例6-2】 压水堆通道热功率阶跃瞬态

问题描述：第二个感兴趣的瞬态问题是在不改变所施加压降的情况下快速增加热流密度。压水堆初始和几何条件见【例6.1】。通道中阶跃施加了一个10%的热流密度增量。

解 压水堆通道内阶跃增加了10%热流密度的SC模型的结果如图6-8所示。可以看出，由于在内部通道点压力上升，减少了入口流量，增加了出口流量。图中示出了20 ms内入口流量减少和出口流量增加幅度的振荡行为。这是因为压力变化在通道中以声速传播，导致各种反射波之间的干扰叠加而导致速度快速变化。

图6-8　采用SC模型计算的压水堆热流密度瞬态时的轴向流量分布

通过MI模型计算的结果如图6-9所示。从瞬态一开始到20 ms，局部流速与平均流速的偏差保持在0.5%以内。

图6-9　采用MI模型计算的压水堆热流密度瞬态时的轴向流量分布

通道中的长期行为（图中未显示）表明：在沸腾时，由于明显的流体局部膨胀，局部质量流速的分布发生变化（但不是平均质量流速）。出口处增加的摩擦限制了出口质量流量的增加。在相对初始状态要低一些的平均质量流速下重新达到稳态。