为了消除声波效应的计算时间步长限制，最好假设流体是不可压缩的（即∂ρ/∂p=0）。在这种情况下，将式（6-4）替换为

式中 p*——系统压力，认为在瞬态期间该值保持恒定。

这个假设在物理上是可以接受的，适用于各种与冷却剂大量损失无关的运行瞬态。由于上述假设，密度变得与当地压力p无关。但密度取决于焓，这意味着流体是热膨胀的。

此外，可以假定在能量方程中，由于压力变化和壁面摩擦力引起的能量传输项可以忽略。因此，式（6-3）可简化为

由于流体不可压缩假设，局部压力梯度不会影响通道内流体的质量流量。实际上，对于等温不可压缩流体，沿通道的质量流量等于入口质量流量，因此质量流量仅由入口和出口压力决定。对于热通道，动量方程仅用于确定轴向平均质量流速G^m，这可以通过求解动量方程（6-2）的积分来获得：

如果定义

式（6-19）可重写为(www.daowen.com)

其中

在F的定义中可包括形损项来考虑入口、出口和格架的影响。在这里，为简单起见，这些项已经在这里忽略掉。因此，动量方程（4-99）给出了估计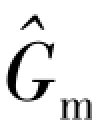的方法。对于Gm随z的变化，根据连续性和能量方程来获得。局部质量流速由连续方程给出

结合式（6-18）和式（6-23），当地质量流速的沿程变化（因当地膨胀）为

上述关于平均质量流速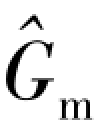方程的差分近似给出了局部质量流速Gm的变化。因此式（6-17）、式（6-18）、式（6-21）和式（6-24）给出了在给定初始和边界条件下确定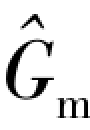（t）、Gm（z，t）、ρm（hm，p*）和hm（z，t）所需的方程，如预期的那样，动量积分法的主要优点是如式（6-16）的限制就没有这么严格，要求时间步长限制为

然而，在动量方程中对密度的近似导致声波在通道中传播所需时间内的信息损失。