动量守恒方程为

方程左边表示体积动量随着时间和对流的变化率。注意左边项乘上的是速度矢量Vk，每一项都有3个部分（uki+vk j+wkk）。基于笛卡尔坐标系，则3个方向共有3个动量方程。方程的右边包括重力项、压力项、黏性和湍流剪切力项，由于相变和夹带引起的动量源项，界面曳力项和由于湍流搅混引起的动量传输项。其中假设压力在所有相中是相等的，重力为体积力。CTF中没有包含湍流剪切模型，所以接下来要把此项从动量方程中消除。湍流搅混使用简单的湍流扩散近似值。

黏性应力项展开成壁面剪切和流体-流体剪切两部分，如下所示：

式中，和分别表示液相、蒸汽相和液滴相的体积壁面阻力。注意在这里假设液滴相不接触壁面，因此没有壁面阻力；通过经验关联式得到。液相—液相黏性剪切应力也没有包含在CTF中，所以也将在动量方程中消掉。

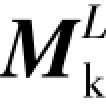项代表由于相变和夹带或者沉积引起的动量源项，其形式如下：(www.daowen.com)

式中，V代表质量流方向的相速度。例如，如果蒸发来自液滴场，然后在动量方程中Γ‴ηVe从液滴动量守恒方程中扣除，同样的动量也需要加入蒸汽动量方程。界面曳力项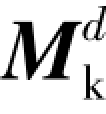对于三相分别展开为：

式中，和为体积相间阻力，分别是蒸汽与液体界面、蒸汽与液滴界面。注意：曳力项对于蒸汽场是负值，对于液滴和液相场是正值。这是因为CTF规定蒸汽相速度比液相和液滴相快，这就意味着界面摩擦阻滞蒸汽相，而拖曳液相和液滴相。如果相反成立，如蒸汽相速度比液相和液滴相慢，则相应的项在CTF中相反。界面剪切力与流型相关，关于该项的计算有不少的模型涉及该问题，但还远未成熟，该问题仍然是目前的研究热点，而且也可能是下一阶段两相流研究的突破之处。

方程（5-106）的最后一项是因湍流搅混和空泡漂移引起的动量源项，。注意，只有轴向方向才有由于湍流搅混和空泡漂移引起的对流项。