在稳态条件下，式（4-119）和式（4-120）中的所有时变项都为零。在单相条件下，LNB=LH，沸腾长度LB以及平均符号（对于G和h）都可以去掉。因此动量方程式（4-119）可以简化为

根据该两项的定义，式（4-121）可以写为

密度与温度的关系可以写为线性关系，即

式中 ρ0——参考温度T0下的密度；

β——热膨胀系数，等于（-∂p/∂T）/ρ。

为简单起见，假设堆芯输入热量和蒸汽发生器排出热量都为均匀热流密度，则对堆芯的热平衡为

因此，冷却剂在堆芯中（加热通道）温升为：

式中 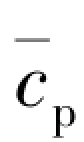——在堆芯温度范围内的平均定压比热。

对于堆芯均匀加热的情形下，在热段（b～e）的温升可表示为：

如果用从加热通道开始的距离来计算，则上式可以写为：

稳态条件下，蒸汽发生器的温降ΔTE是等于ΔTH的。

可以将浮力项重新整理成回路中与最大密度差及加热中心和冷却中心高差的关系。因为浮力水头是沿回路沿程对重力项进行积分得到的，可以把该项写为：

但在右边第一项中，dT/dz为常数，dρ/dT在单相流中可以近似的处理为常数，所以密度沿z向线性变化，则第一项积分可写为

对于第二项积分，密度ρ为常数，因此有：

对于第三项积分，假设在e和f之间，ρ沿z向线性增加，在f和g之间也是同样情况。因此有

因为ρe=ρc，ρg=ρb，所以有

式（4-123）的最后一项为(www.daowen.com)

将以上关系代入式（4-123）得到：

因为，则上式变为

式中，。也就是说，ΔL为反应堆系统冷热芯之间的高差。因此有

应用密度和温度的关系，得到

对于以上三式的物理解释可以是：浮力水头等于冷却剂沿回路最大密度和最小密度之差在高度上的作用水头，或者是冷热芯高差的作用水头。最大密度和最小密度分别发生在热排出和热输入的位置。该描述对于其他的轴向热输入输出的浮力水头都是相同的描述。

摩擦阻力可以写为如下的形式：

式中 m·——回路的质量流率；

CR=R（m·）-n——水力阻力系数；

R——计算阻力系数时的比例常数。在湍流下，n=0.2，层流时n=1。因此有：

将Δpf和ΔpB的关系式代入式（4-121），并假设在回路中温度变化相对于密度变化很小，因此ρ0≈ρf，可以得到

式中 ρ0——参考冷却剂密度。因此，对于给定温差，得到回路的质量流率为

在给定加热功率Q·H下，将ΔTH的关系式（4-122）代入式（4-126）得到

需要注意的是，在实际的反应堆系统中，堆芯内温度并不是线性上升的，在换热器内温度下降可能接近于指数形式。因此，求解反应堆系统的精确方程需要借助于数值手段。Zvirin等显示精确解和线性温度分布假设之间的误差很小，在m·和ΔTH上只有5%左右。

在给定允许ΔTH下，在确定的系统结构条件下，通过自然循环能带出的最大功率可通过将式（4-128）代入式（4-127），重新整理得到

可以看出对系统排热能力影响最大的因素是ΔTH、cp和ρ0，而ΔL和R的影响相对较小。