首先基于图4-29导出一维回路流动方程。该回路具有单相和两相堆芯条件的所有必要的特征，包括：

①在代表堆芯的LH长度内热量加入热段中。

②对于有沸腾的情形下，沸腾在ZB处开始发生，沸腾长度为LB。

③堆芯上部的L′B不提供热量输入，代表燃料棒上部的堆腔或者反射层位置。

④冷却发生在冷边热交换器的2LE长度内，代表回路中简化的U形管蒸汽发生器。

对于与z轴夹角为θ的轴向不变流通面积的一维流动的守恒方程包括：

动量方程：

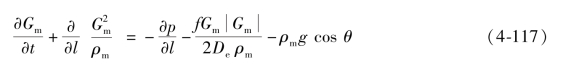
能量方程：

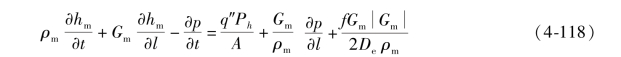
上述方程中，l表示沿通道轴向的流动方向，可能不是一直是竖直方向，f为对应于当前的单相或两相流型的摩擦阻力系数。

将式（4-117）的各项按照图4-29的回路从泵的a点开始积分，到泵的入口点i点结束。先从右边第一项开始。

静压的积分为

式中 Δp泵——运行条件下为正；而因阻力损失，泵在静止条件下为负。

令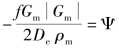，则对阻力项在堆芯和堆腔内、蒸汽发生器以及回路的其余部分进行分段积分得到：

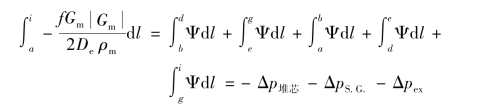
式中，Δpex为除了堆芯和蒸汽发生器之外回路的损失。注意Δp堆芯、Δpex和ΔpS.G.为正值，代表了沿回路流动方向压强阻力损失的大小。当只在重力项考虑相密度的变化时，f和Gm在定面积加热通道中就成为与位置无关的量，则

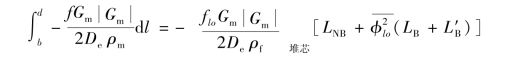
注意如果在堆芯通道中存在某些局部阻力件时，则上式修改为：

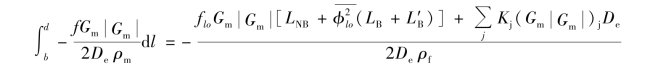
式中 Kj——在通道中的j位置的局部阻力系数。可以是单相，也可以是两相。

重力项积分为(www.daowen.com)

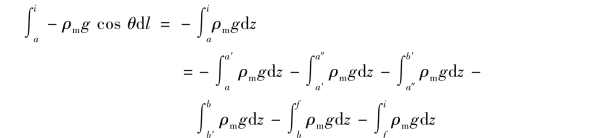
式中，dz=cosθdl。

可以很容易看到，当忽略压降对每项的密度变化，ρm仅因为在堆芯和蒸汽发生器的加热或冷却而受到影响。因此在绝热段a′～a″和b′～b都有相同的位头，a和a′两点z向位置都相同，因此上式右边的第一、第二和第四项都为零。因此上式简化为

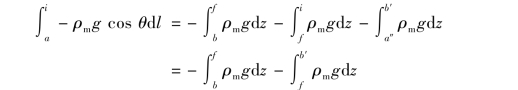
因此在整个回路对重力项积分得

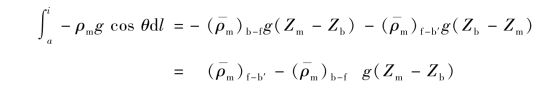
其中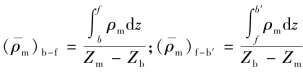，。因此，重力的净浮力是由热边和冷边的平均密度不同所导致，它的值等于密度差乘以有密度差的总高度。

考虑式（4-117）的左边各项，将第一项积分得到回路中冷却剂的时间加速项：

式中，Lk为具有定常面积Ak的k流段的长度。

对于空间加速项，有

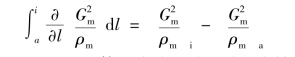
如果泵两边的接管面积相同，通过泵后流体的密度不变，则上式结果为零。

忽略局部阻力损失，回路的动量方程可写为：

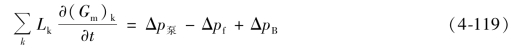
式中 Δp泵——泵的压头；

Δpf——整个回路的摩擦压力损失，分为堆芯、蒸汽发生器和其他的外部压头损失等，因此有：

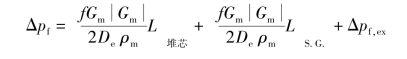
ΔpB为浮力水头，即

对于能量方程，压力变化和摩擦耗散所导致的能量改变可以忽略；在压力变化不大的情况下，∂p/∂t可以忽略。在堆芯及蒸汽发生器之外的焓变化可以忽略，因此，基于图4-29，式（4-118）可以变为

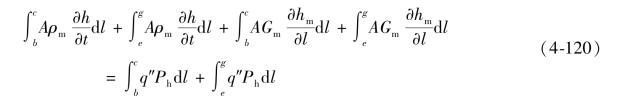
尽管上述方程既可以用于两相，也可以用于单相，但需要注意的是许多反应堆系统工作于单相状态（PWR，LMR和HGTR）。只有在一些严重瞬态条件下，压水堆一回路的蒸汽发生器或液态金属堆的换热器才有两相。因此，先分析单相条件，然后再用类似的方法分析两相条件。