该方法有两个基本假设：

①在两相流流场中，常用的单相压降关系可以分别用于两相压降的计算。

②在轴向位置两相压力梯度相同。

在前面的讨论中，我们将摩擦压降与具有相同质量流速的单相压降联系起来。另外还有一个方法是沿通道的摩擦压降可以通过在通道内分别流动的两相的流动来预测。因此

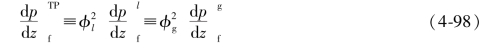
式中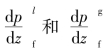，分别为液相和气相以它们的实际流率单独通过通道的压降。则根据定义有

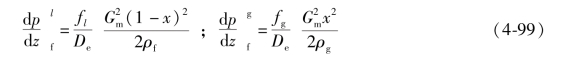
因此有

从式（4-77）和式（4-100），有

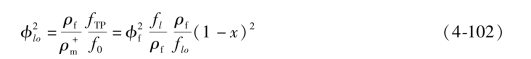
因为Relo=GmDe/μf，Ref=Gm（1-x）De/μf

摩擦阻力系数与相应的雷诺数的关系可以写为

式中，n=0.25或0.2，依据选取的模型不同而不同。将式（4-103）代入式（4-102），得到

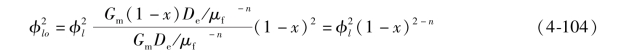
Lockhart和Martinelli定义了一个参数X（目前称为Martinelli参数）为：(www.daowen.com)

注意从式（4-98）中可知，X2=φ2g/φ2

l。将式（4-99）和式（4-103）代入式（4-105），当取f与Re-0.25成正比时（n=0.25），得到热平衡条件下的X2。

如果取f与Re-0.2成正比时（n=0.2），得到

Lockhart和Martinelli建议φl和φg可以关联为关于X的单值函数。图形关系示于图4-23中。他们的结果是根据低压下水平绝热两组分系统流动的数据得到的。他们的曲线可以用下面的关系式来拟合：

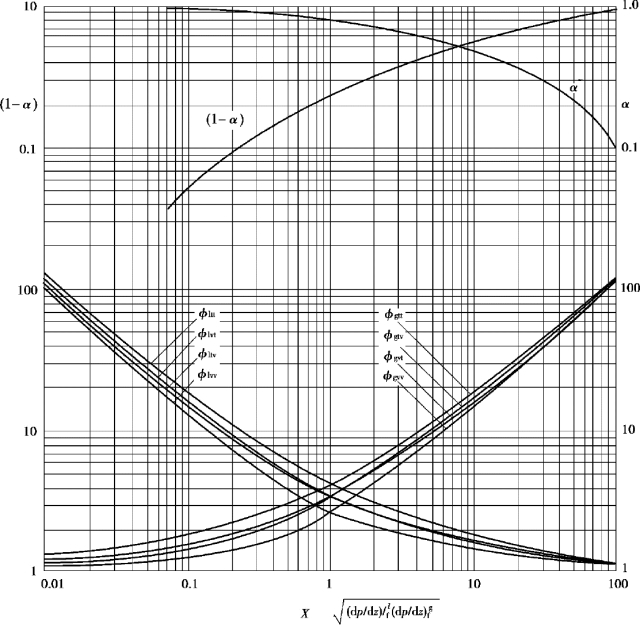
图4-23　压强梯度比率和空泡份额的Martinelli模型

C的取值见表4-9所列，与某相的流动是处于层流或湍流的流态有关。在实际使用中，如果考虑流态的变化所导致的φ2g和φ2l的数据分散比实验值大，因此一般对所有流态都用C=20的值（即只考虑湍流-湍流工况）。

根据式（4-108）和式（4-110）也隐含了下述条件

该式也被Chisholm理论推导得出。

表4-9　各流态组合下常数C的取值