均相流模型假定液相和蒸汽的速度相等，两相处于热力学平衡状态，它们的速度为

对于均相流模型有（或者任何模型假设两相速度相等的情况下）

将式（4-73）和式（4-74）代入式（4-75），得到

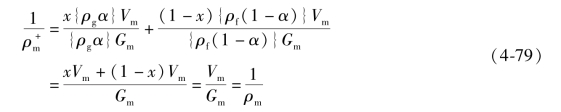
式（4-79）表明，在均相流模型中，动力密度等于混合物密度，即

对于均相流，考虑到动力密度与混合物密度相等，因此有

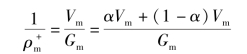
因此根据干度x的定义，得到

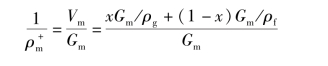
对于均相流有

因为Gm在等截面管中不变，则均相流模型加速压降写为

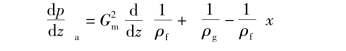
或者

如果vg和vf与z无关，也就是说液体和气体都假设为不可压缩，则有

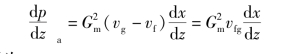
当只忽略液体的压缩性时，则为

对于均相流，摩擦压降梯度的式（4-76）变为

因此，综合上述的式（4-68）、式（4-70）、式（4-82）和式（4-83），并重新整理得到

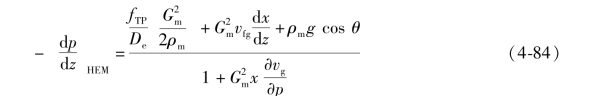
（1）McAdams平均黏度

(www.daowen.com)

（2）Cicchitti平均黏度

（3）Dukler平均黏度

为了计算由式（4-77）定义的两相摩擦压降倍数φ2lo，可以采用下面两种近似方法：

①假设fTP等于与两相总质量流量Gm相同的液相单相流的摩擦系数：

②假设两相流的fTP与雷诺数的关系与单相的flo关系相同，因此有：

-（dp/dz）lo表示把整个流体都当作液体时由达西公式计算得到的全液相压降梯度，即-（dp/dz）lo=f0G2mvf/2D。其中f0为全液相摩擦阻力系数。写成一般的形式则为

式中 φ2lo——两相摩擦压降倍数。

由式（4-77）定义，均相流模型下，根据式（4-88）的条件可以写出

在热力学平衡条件下，式（4-91）变为

如果采用式（4-89）的假设，并基于式（4-85），得到

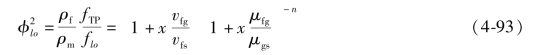
假设两相摩擦阻力系数按Blasius关系式用黏性系数表示为

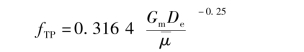
如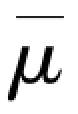用式（4-85）求值，则可得到下面的两相流摩擦压降梯度的表达式：

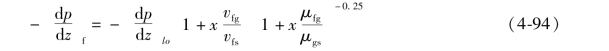
式中，μfg为气液两相的黏性系数的差值，即μfg=μf-μg。因此有

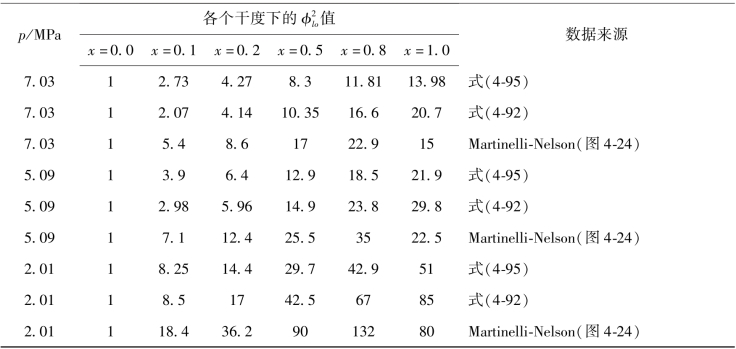
表4-8列出了用各种模型计算得到的两相摩擦压降倍数φ2lo的值。可以看到模型之间差异比较大，在选用模型时需要根据工况及物性参数条件选择适当的模型计算。

表4-8　用各种模型计算的汽水混合物的φ2
lo值