这里我们先基于均相流模型讨论压降，然后再基于非均相流模型来讨论。此外，在这里需要强调的是，在两相流中大量采用经验关联式的现象不足为奇，因为两相流本身就是一个非常复杂混乱的流动。

压降梯度可以通过两相混合物在z方向一维通道的动量方程来计算

式中 θ——流动方向与竖直向上方向的夹角。

对于在截面不变通道内的稳定流动，上式可以简化为

该式中，假设通道的径向压差可以忽略。

上式表达了通道中总压降梯度的组成，分别为加速压降梯度、摩擦压降梯度和提升压降梯度等3部分组成，即

式中各项分别为

式中 τw——剪切应力的周向平均；

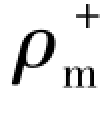——动力密度。

注意在流动方向dp/dz为负，（dp/dz）f始终为负值。另外两项的符号与通道条件有关。对于加热通道，ρm在z方向降低，则（dp/dz）a为正值。如果cosθ为正，则（dp/dz）el为正值。

为了得到具体的压降，需要对压降梯度方程进行积分：

或者

式中(www.daowen.com)

如果基于每相的质量流速写出动量通量，动力密度ρ+m可以写为与流动干度的关系。因为

流动干度可以由下式得出

则有

式中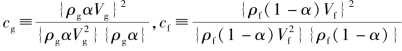，。对于各相在流道中径向分布均匀的情况下，cg=cf=1.0。这种情形下，式（4-74）变为

对于均匀速度分布，在考虑加速压降时忽略径向分布的不均匀性。

两相流摩擦压降梯度可以表达为与单相相似的如下形式：

式中 ——水力当量直径。

两相流摩擦压降梯度dp/dz　f的表达式一般都定义为同样总质量流速的单相流摩阻系数flo与两相流摩擦压降倍数φ2

lo的关系，如果是对于蒸汽的参数分别为fgo和φ2go。这些参数之间的关系为：

因此有

一般情况下，在沸腾通道中使用“全液相”参数，而在凝结通道中使用“全气相”参数。因此在两相沸腾通道中的摩擦压降梯度表示为：