关于滑速比更为通用的关系是Zuber和Findlay考虑通道内平均速度的漂移流模型。首先，将气相速度表达为混合物的表观速度和气相当地漂移速度的和。因此有

因此对于气相的表观速度jg有

将该式在断面上平均，得到

注意到右边第二项是用漂移速度来定义的。在物理上它表示气相以速度j从单位面积（与通道的轴向正交）上通过的流率。则气相的表观速度可以从式（4-58）得到

式中分布参数C0定义为

有效漂移速度定义为

式中的{α}可以根据式（4-58）得到

可以认为空泡份额受两个因素的影响，则式（4-61）可以写为

式中，C0项代表由径向的空泡和速度分布不均所导致的全局效应。

而Vgj/{j}项代表当地相对速度效应。在较高速度下，当地效应可以忽略，也就是说相对速度可以忽略（即Vgj≈0）。该条件在蒸汽-水系统中可以使用，这也是Armand和Treschev以及Bankoff等模型所隐含的条件，该条件可以写为：

式中的常数K定义为

(www.daowen.com)

对于均相流，不考虑当地滑移，也不考虑径向的分布效应，因此C0=1，有

当地滑移比较小时，Armand和Treschev建议

式中的p的单位为MPa。Bankoff建议

式中的p的单位仍为MPa。

Dix提出了一个关于适用于各种流型的C0的表达式

式中，b=（ρg/ρf）0.1。

如果采用质量流量和干度来表达式（4-61），则有

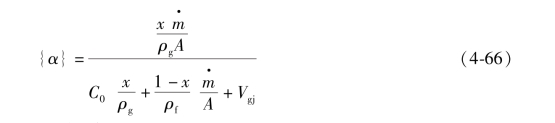
比较式（4-66）和式（4-35），可以得到

对流通截面上空泡均匀分布的情形，C0=1。Zuber和Findlay建议C0和Vgj为流型的函数。泡状流和弹状流C0=1.2，空泡份额接近于0时，C0=0，在高空泡份额时C0=1。而泡状流和弹状流的漂移速度Vgj可表示为

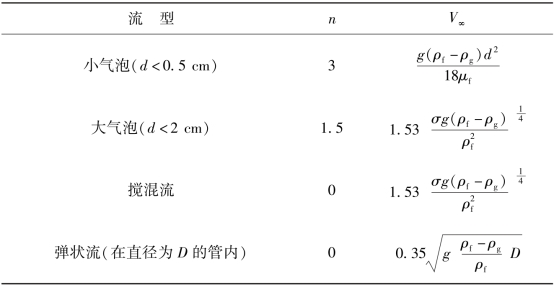
式中 V∞——气泡上升的终端速度，终端速度和n的取值见表4-7。需要指出的是，在泡状流时因为有其他气泡存在，其漂移速度比终端速度低。而在弹状流和搅混流中与V∞相同。

表4-7　各种流型的n和V∞

Ishii将漂移流关系延伸到环状流。然而在环状流中气相的体积流率与总体积流率有一些差异，Vgj并不显著。