液泛和流动反转在几个重要的反应堆热工水力现象中会遇到，包括流型转变和在轻水反应堆失水事故（LOCA）中热表面的再润湿现象。液泛是指由于向上流动的气相速度足够高，使向下流动的液相停滞；而流动反转是指开始时液相与气相同向向上流动，而当气相速度降低到某个足够低的值后，发生液相流向转向。尽管已经开展了一些实验来预测液泛和流动反转，但到目前为止仍没有统一的理论。针对该问题国际上已经开发了一些经验关联式可以用于工程设计中。在这里我们将针对简单几何结构来分析该问题。

图4-15示出了液体注入设备中的竖直带多孔壁面的管道。开始时气相流速为零，液膜按恒定流速向下流动。气体流速逐渐增加，在管内保持两相逆向流动（管1）。当气相流速增加，液膜厚度保持常数，数值上等于Nusselt于1916年所给出的层流液膜厚度。该无因次液膜厚度表示为

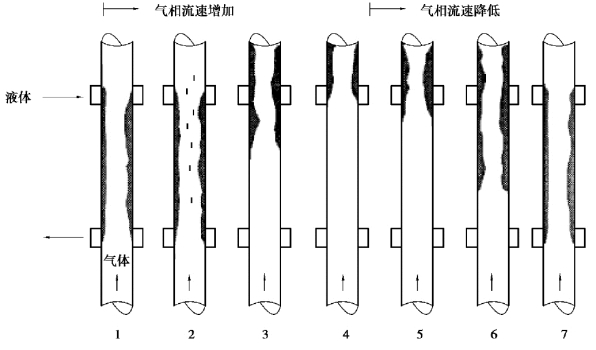
图4-15　液泛和流动反转实验

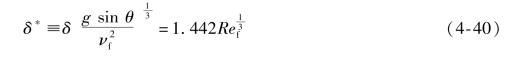
式中

θ——与管轴与水平方向的夹角；

νf——液体的运动黏度；

Qf——液体的体积流量；

D——管子直径；

g——重力加速度。

该关联式在Ref小于2 000时有效。对于湍流液膜，其厚度可以表达为：

随着气相流速增加，液膜变得不稳定，出现较大幅度的波，有效液膜厚度增加。波峰上的液体被撕裂为夹带液滴，并被气相夹带到注入点之上，一些液滴碰撞到壁面使液膜厚度增加，这时就出现了液泛现象（管2）。同时，液体注入口上部管段的压降损失急剧增加。随着气相流速继续增加，注入口以下的管段的液膜逐渐干涸（管3）；当向下流动的液体完全被阻止，该点就称为完全液泛条件（管4），也称为逆向流动限制（CCFL）条件。在更高的气相流速条件下，在上部管段出现搅混流或环状流等流型。

如果这时候逐渐降低气相流速。在某个数值时液膜变得不稳定，在界面上出现大幅度的波，压降增加，液膜开始逐渐回落到注入口之下。该点称为流动反转现象（管5）。继续降低气相流速，液膜继续往下回落，直到某个气相流速下上部管道完全干涸（管6）。

图4-15示出的实验总结在图4-16中。注意液相从向上流动转变为向下流动之前会经历向两个方向流动的过渡期，反之亦然。

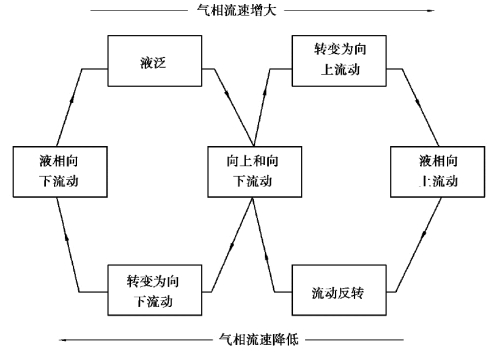
图4-16　液泛和流动反转

关于逆向流动限制和流动反转问题，普遍采用两个无因次数来关联这个两相流的转变过程：Wallis数和Kutateladze数。前者表示惯性力与作用在直径为D的气泡或液滴上的静压力。后者将尺度D替换为拉普拉斯常数

Wallis数定义为：

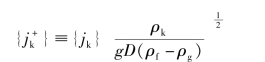
其中，k表示液相的f或者气相的g，式中{}符号表示截面平均。(www.daowen.com)

而Kutateladze数（Ku）的定义为：

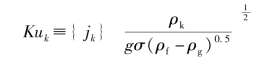
Wallis提出了竖直管内液泛的关联式，与通道的尺寸有关，即

式中 m，C——常数，与管道出口的形式有关。

圆管的m=1.0，圆滑出口C=0.9，而直角管出口为0.725。在实际应用中，这两个常数对不同的几何结构根据实验确定。

Porteous给出了半理论的逆向流动限制条件：

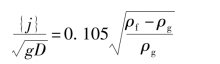
对于流动反转，Wallis建议：

后来Wallis和Kuo修正了该流动反转的关系让它与实验数据更加一致，显示它与管子直径的关系并不是很大。

在分析了直径为6～309 mm的管内空气-水的实验结果后，Pushkin和Sorokin提出流动反转在Kutateladze数为3.2时发生：

他们所提出的该条件与液泛条件很相近。

逆向流动限制现象还被其他多个作者所分析，总的来讲，可以将逆向流动限制触发的条件解释为4种物理机制：

①液膜驻波机制。

②两相相对速度所导致的界面不稳定性。

③液膜净流量为0。

④从液膜撕裂的液滴夹带起始机制。

流动反转现象与液膜的流体动力学特性密切相关。Bankoff和Lee对现有的竖直和水平逆向流动的液泛和流动反转实验和分析研究有深入的评述。因为对各个现象的起始有多种定义，在应用这些经验关联式之前需要仔细检查其应用条件。图4-17给出了竖直逆向流动的压降特性的实验数据。

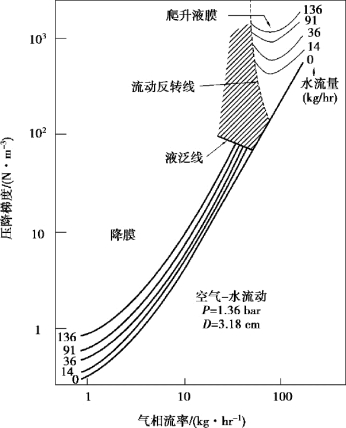
图4-17　竖直逆向流动转变的压降特性