当气体冷却剂在通道内作等温流动时，如果气体的压力变化不大，例如进出口压力比pin/pex≈1，则因此时气体的密度变化很小，就可以把流速看作常数。在这种情况下，可以认为气体冷却剂也和液体冷却剂一样，在通道内只存在提升压降和摩擦压降，于是根据式（4-2）、式（4-4）就可以算出气体冷却剂的流动压降。在一般情况下气体的密度是很小的，气体位能改变所引起的提升压降与总压降相比也是非常小的，因此在计算气体的流动压降时，为了简化计算，往往忽略这一压力变化项。

在堆芯冷却剂通道（或热交换器内的冷却通道）内，当气体被加热或冷却时，其体积要发生显著膨胀（或因被冷却而收缩）。气体体积的膨胀，往往导致气流明显加速。因此，气体冷却剂沿等截面加热（或冷却）通道流动时，除了气体的摩擦压降之外，还存在着因体积改变而产生的加速度压降。在加热通道内，气体密度变化的主要原因是气体温度改变；除此之外，气体的压力沿流动方向不断发生变化也是造成气体密度变化的一个原因。下面以气体在水平通道内的加热流动为例，具体分析其流动压降的计算方法。

图4-12表示一个长度为L，流通截面积为A的等截面加热通道。进口处气体的压力为pin，温度为Tin，相应的密度为ρin，流速为Vin。在通道内气体被加热，出口处气体的温度上升到Tex，相应的密度变为ρex，流速变为Vex，气体的压力下降到pex。

图4-12　气体沿等截面加热通道流动时的压降

在离进口距离为x处取一个厚度为dx的通道体积元，考虑到摩擦力的作用，根据动量定理，对体积元内的气体可写出如下的方程：

式中 dpf——由于摩擦引起的作用在体积元单位横截面积上的阻力。

根据达西公式，有

把dpf值代入上式整理后得到

式中 f——摩擦阻力系数；

De——通道的当量直径，m；

ρ——截面x处气体的密度，kg/m3；

V——截面x处气体的流速，m/s。

式（4-22）两边同时乘以压力p得到

对上述方程沿通道全长积分，可以写出

式（4-23）左边的积分项给出

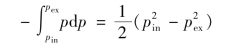
对式（4-23）右边两项进行积分时，考虑到下述各种关系：

①通道气流的连续性。根据连续性方程得G=ρinVin=ρexVex=ρV。式中的G是气体的质量流速，kg/（m2·s）。(www.daowen.com)

②气体摩擦阻力系数f通常与Re-0.2成正比，对于等截面通道，黏性系数μ是唯一能够引起雷诺数沿通道长度方向发生变化的参量。一般来说，气体的黏性系数受温度变化的影响并不明显，因而气体温度变化对摩擦阻力系数的影响也十分微弱。这样，在积分时就可以把f作为常数看待。通常按通道进出口温度的算术平均值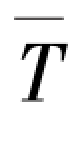 =（Tin+Tex）/2来计算f值。

③对于反应堆的情况（压力不算太高，温度不算太低），可以把气体冷却剂当作理想气体处理，即认为它服从理想气体状态方程式

式中 p——气体的压力，Pa；

v——气体的比体积，m3/kg；

R——气体常数，R=8.314×103/M，J/（kg·K），这里M指气体的相对分子量；

T——温度，K。

由式（4-23）右边第一项的积分给出为

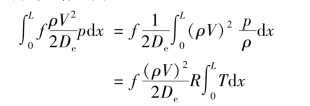
如果热流密度的分布与通道的中心相对称（这是反应堆冷却剂通道经常碰到的情况），则

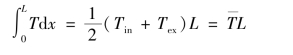
应用该式结果，可得到

式（4-23）右边第二项的积分给出

如果用通道的平均温度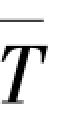代替上述方程等号右边积分项中的T，则可以得到

把以上各项的积分结果代入式（4-23）得到

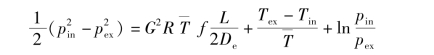
用（pin+pex）/2除方程两边，便得到气体冷却剂在受热直通道中压降的表达式为

式中 ρ——在平均压力p =（pin+pex）/2和平均温度T下的气体的平均密度，可由理想气体状态方程式求得。

式（4-24）等号右边第一项表示摩擦压降；第二项表示由温度升高引起的加速压降，对于大多数气冷动力堆来说，它的数值占总压降的10%～15%；第三项代表由压力降低引起的加速压降，它的数值很小，仅占上述总压降的1%～2%。

应该指出，式（4-24）的右边也包含有未知数pex，因此用式（4-24）求解通道出口压力时，往往需要进行迭代计算。其步骤是先假定一个出口压力p′ex，根据该值用式（4-24）算出一个pex，然后将算出的pex和p′ex进行比较，如果两个值不等，那就将本次的pex设为p′ex再次进行计算，直到两个值的差值在允许的误差范围内时为止。