（1）层流流动

在前面对单相流动摩擦压降的讨论中我们谈到，沿非圆通道层流流动的阻力计算不能采用当量直径作为定性尺寸的计算方法。可采用如图4-3所示包围在棒束表面的环管的替代方法。

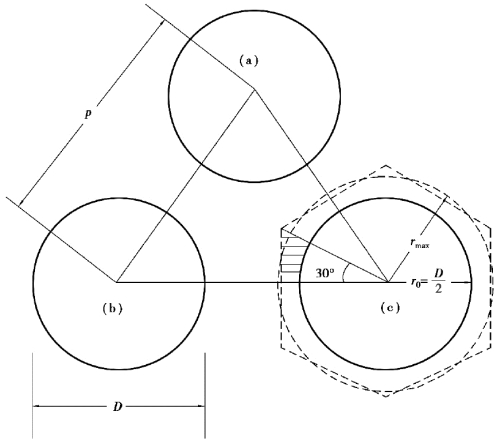
图4-3　三角形燃料栅元的等效环管定义

剖面线区域表示元件的冷却剂区域，rmax的圆代表相同流通面积的等效圆环。这里用Re′表示光棒通道的雷诺数，后面用Re表示带定位格架的雷诺数。

在这里，用Re′表示没有定位格架的光棒的雷诺数。图4-4示出了Sparrow和Loeffler给出的在三角形通道中等效环管充分发展层流下fRe′De与P/D的关系。可以看到，当P/D大于1.3时，等效环管模型吻合很好。Rehme得到了完整的棒束层流的数据，Cheng和Todreas采用多项式对每个子通道的数据进行了拟合，拟合的形式为

fiL≡C′fiL/Re′n iL，这里，i表示第i种子通道，L表示层流，后面将用T表示湍流。对于层流，n=1。如对边通道和角部通道使用式（4-14），则用W/D代替P/D，W为棒直径加上棒与棒束盒壁面的距离。P/D（或者W/D）的效应分为两个区域：1.0≤P/D≤1.1及1.1≤P/D≤1.5。表4-5给出了方形栅元的a，b1和b2值。

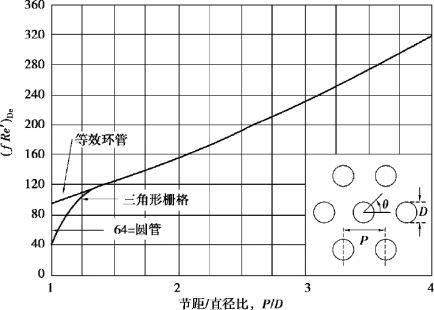
图4-4　棒束通道内顺流层流摩擦阻力系数和雷诺数的乘积与节径比的关系

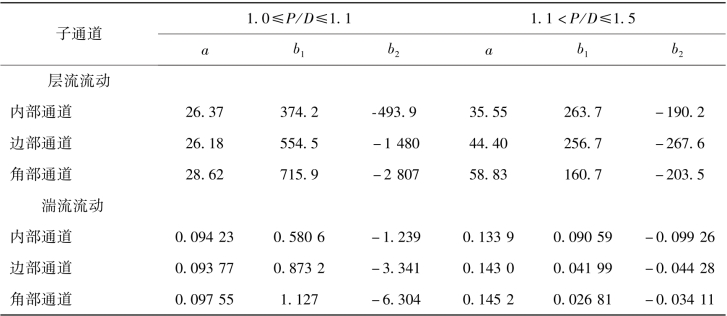
表4-5　式（4-14）中计算光棒束子通道阻力因子常数C′fiL的系数

假设所有子通道压力均匀，通过总的棒束质量流量的平衡分配到各子通道中得到平均的子通道摩擦因子。得到：

式中 Si——第i种类型的子通道的流量在总流量中的份额。

图4-5示出了用式（4-15）计算的37棒束组件与现有的层流（n=1）结果的数据的比较情况。

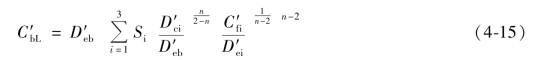(www.daowen.com)

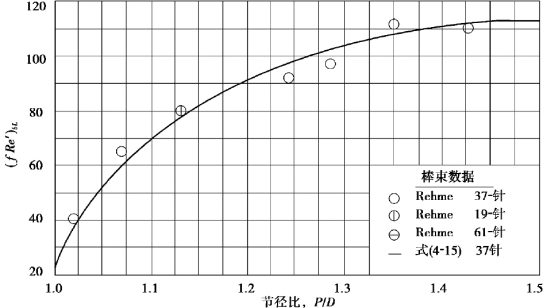
图4-5　三角形栅元光棒的层流摩擦阻力数据

（2）湍流流动

早期的关于湍流区的研究包括Deissler和Taylor的工作，他们依据早期测量的通用速度分布推导出了摩擦因子。根据当量直径概念，用他们的方法得到的结果与节径比P/D=1.12、1.20和1.27的方形和三角形棒束栅元进行了比较。结果显示在Re>105时，式（4-6）在一定的分散度内可以用于预测。然而，这些数据显示摩擦阻力与P/D的关系不能用当量直径的概念借助于圆管的关系式来预测。LeTourneau等测试了P/D为1.12和1.20的方形栅元棒束和P/D为1.12的三角形栅元的棒束，在雷诺数为3 000～3×105区间，这些数据与光滑圆管结果的误差在10%以内。

后来，Trupp和Azad得到了三角形棒束栅元中空气流的速度分布、涡扩散和阻力因子。这些数据显示阻力因子比Deissler和Taylor预测值高。在雷诺数为104～105区间，在P/D=1.2时，他们的数据比圆管数据高17%。P/D=1.5时要高27%。

对于湍流流动的情况，求解棒束或者等效圆环精确的流动都需要知道湍流速度分布。对于三角形栅元，Rehme得到了如下的等效圆环的解：

对于Re′De=104：

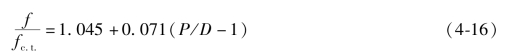
对于Re′De=105：

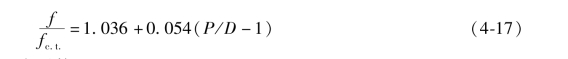
式中 fc.t.——圆管的摩擦阻力系数。

Rehme还提出了一个求解实际几何尺寸的方法。Cheng和Todreas采用式（4-14）的多项式形式进行了拟合，则为

其中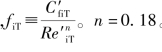。同样采用表4-5给出的a，b1和b2值。而棒束湍流摩擦因子C′bT可以通过式（4-15）求得。图4-6比较了37棒束的相关数据，可以看出，吻合较好。

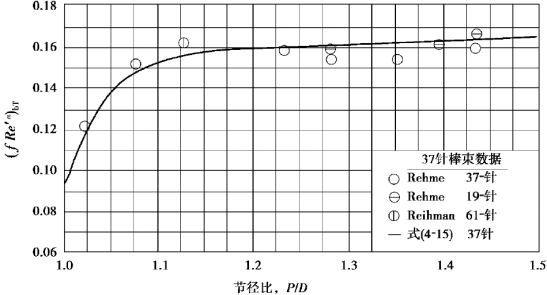
图4-6　三角形栅元光棒湍流的摩擦阻力数据