计算单相流的摩擦压降，普遍采用达西（Darcy-Weisbach）公式，即

式中 Δpf，l——摩擦压降，Pa；

f——摩擦阻力系数（量纲为1）；

L——通道长度，m；

De——通道的当量直径，m；

ρ——流体的密度，kg/m3；

V——流体的速度，m/s。

式中的f称为Darcy-Weisbach摩擦阻力系数。它与流体的流动性质（层流与湍流）、流动状态（定型流动即充分发展的流动与未定型流动）、受热状态（等温或非等温）、通道的几何形状、表面的粗糙度等因素有关。

（1）等温流动的摩擦阻力系数

①圆形通道。流体在圆形通道内作定型层流流动时，其摩擦阻力系数完全可以用解析法给出，其结果为

式中 Re——雷诺数，流体在圆形通道内作层流流动时，Re<2 320；

μ——流体的黏性系数，Pa·s。

若流体作湍流流动，沿通道流通截面上的流体速度的分布规律比较复杂，要用解析方法导出求解摩擦阻力系数的关系式相当困难。在一般情况下，湍流摩擦阻力系数关系式只能通过实验确定。

对处于光滑的圆形通道内定型湍流的情况，常用的关系式有：

McAdams关系式（30 000<Re<106）

Blasius关系式（2 300<Re<30 000）

当Re>100 000时，可采用Karman-Nikuradse关系式进行计算

管子的相对粗糙度（ε/D）会提高有效的摩擦阻力系数。最常用的方法是采用如图4-1所示的Moody图来确定摩擦阻力系数。Moody图可以用Colebrook的经验公式来表示：

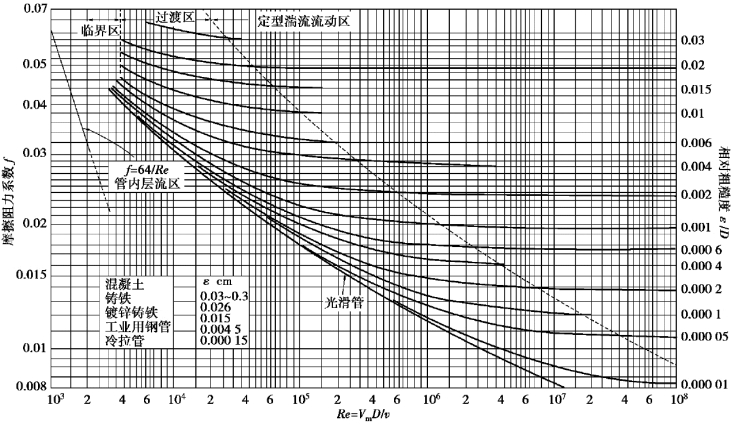
图4-1　莫迪沿程摩擦阻力系数

式中 D——通道的直径，m；

ε/D——相对粗糙度；

Re——雷诺数；

ε——通道表面的绝对粗糙度，其典型数值见表4-1。

表4-1　常用管道表面的绝对粗糙度

(www.daowen.com)

②非圆形通道。非圆形通道的层流摩擦阻力系数，具有和圆形通道相类似的数学表达式，其一般关系式为

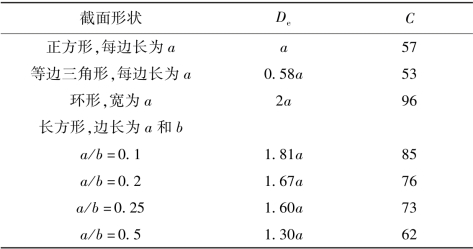
式中的常数C与通道截面的几何形状有关，它们的数值列于表4-2中。

如果用非圆形通道的当量直径代替圆形通道的直径，那么就可以直接应用圆形通道的关系式来计算非圆形通道的湍流摩擦阻力系数，或者从莫迪图中查得f。当截面形状越接近圆形时，用De计算的结果误差越小，反之则越大。

对于光滑通道，若雷诺数在104～2×105的范围内，则实测得到的三角形截面通道的f值要比莫迪图给出的值约低3%，而实测的正方形截面通道的f值要比莫迪图给出的值约低10%。对于狭窄的光滑矩形通道，如板型燃料元件的情况，其f值与圆形截面通道的值相同；然而对于粗糙的矩形通道，实测的f值要比相同粗糙度条件下莫迪图给出的值约低20%。沿棒状燃料元件的纵向流动，属于平行流流过光滑棒束的流动，这时f值不仅与雷诺数和栅格的排列形式有关，还与棒间距P和棒径D之比（即P/D）有关。用P/D为1.12的三角形栅格以及P/D为1.12和1.20的正方形栅格进行实验所得到的数据表明，与莫迪图中的光滑圆管曲线相比，都存在不同程度上的差别。

表4-2　几种非圆形通道的当量直径De和常数C的数值

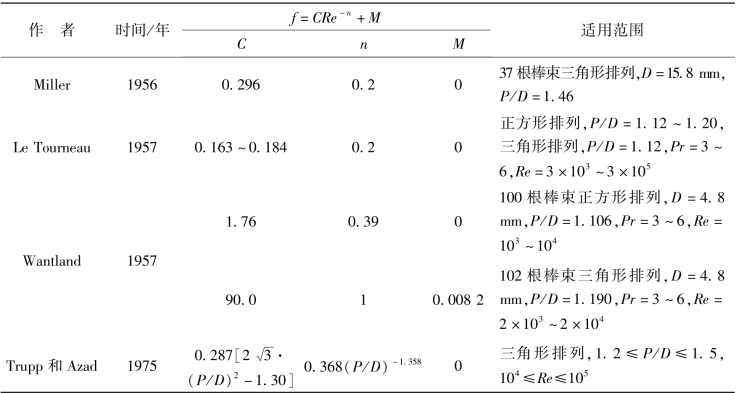
迄今为止，对棒状燃料组件的摩擦压降进行了大量的实验研究，但由于实验都是在特定条件下进行的，受到棒的数量、直径、长度、P/D以及运行工况的限制，因此所得到的经验公式往往带有较大的局限性，远不能包括反应堆工程领域内可能遇到的多种多样的情况。表4-3列出了几个在特定条件下计算棒束摩擦阻力系数f的经验公式。在缺少可靠实验数据的情况下，通常采用计算圆形通道摩擦阻力系数的公式来估算棒状燃料组件的摩擦阻力系数。

表4-3　几个计算棒束摩擦阻力系数f的经验关系式

（2）非等温流动的摩擦阻力系数

前面介绍的求解摩擦阻力系数的关系式和莫迪图，只对等温流动适用。所谓等温流动，是指流体在流动过程中，其截面上所有各点的流体温度都保持一致，且沿程不变。但在有热交换的场合（如反应堆堆芯或蒸汽发生器），流体被加热或冷却，在这种情况下，流体的温度不仅沿截面变化，而且沿着通道的长度方向也有变化，这时流动便成为非等温流动了。随着热量的传递，在靠近管壁的边界层内出现了较大的温度梯度。和等温流动相比，流体受热时，近壁温度比主流温度高，黏性系数则较低；当流体冷却时，情况则刚好相反。

考虑到边界层内流体黏性系数的改变对摩擦压降所产生的影响，式（4-4）在用于非等温流动的计算时，需要作出适当的修正。其中除了摩擦阻力系数必须作相应的修正或采用专门的公式计算外，还要考虑到从通道进口到出口流体温度不断改变所引起的物性变化。涉及温度改变的影响所采取的办法是，用流体的主流平均温度来计算流体的物性。该温度为

式中 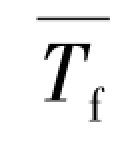——流体的主流平均温度；

Tf，in和Tf，ex——分别表示流体的进口与出口主流温度。对于液体，非等温流动湍流摩擦阻力系数大都采用Sieder-Tate所建议的方程计算。该方程为

式中 fno——非等温流动的摩擦阻力系数；

fiso——用主流平均温度计算的等温流动摩擦阻力系数；

μw——按壁面温度取值的流体的黏性系数，Pa·s；

μf——按主流温度取值的流体的黏性系数，Pa·s。

对于压力为10.34～13.79 MPa的水，Rohsenow和Clark的实验表明，若只考虑摩擦损失，Sieder-Tate方程中的指数n应取0.24。

与非金属流体相比较，液体金属的热导率高，黏性系数低，在加热或冷却时边界层内的流体温度与主流温度相差很少。对于这种情况，在计算摩擦阻力系数时，可按等温工况考虑。

（3）通道进出口效应对摩擦阻力系数的影响

以上所给出的摩擦阻力系数数值都是对定型流动（不论是层流还是湍流）而言的。进入通道的流体是不能立刻达到定型流动状态的，而需要在通道内流过足够长之后才能达到。这段长度称为进口段长度（图4-2中的Le）或稳定段。在进口段长度内，流体的流动特性和速度分布都要发生很大的变化。与定型流动相对应，通常把进口段长度内的流动称为未定型流动。

在进口段长度内，流体的流动尚未定型，这时流体的摩擦阻力比定型流动的要大。这是因为：

①在进口处速度分布是近乎均匀的，因而在紧贴壁面的边界层内形成了较大的速度梯度，由此导致较大的壁面剪应力。

②速度自进口处的近乎均匀分布转变为稳定分布减少了流体的动量通量。因此不能用定型流动的摩擦阻力系数计算进口段长度内的摩擦压降。在进行具体的摩擦阻力系数计算时，必须弄清楚所处理的是不是定型流动，忽略这一点可能会给计算结果带来较大的误差。

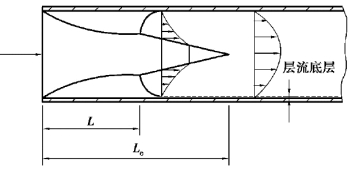
图4-2　进口段对流速分布的影响

根据很多的实验结果，得出了流体达到定型流动时的进口段长度Le为：湍流时Le≈40D；而层流时Le=0.028 8DRe；D是通道的直径。

未定型流动的摩擦压降，目前还没有可供使用的精确计算表达式，通常需要由实验给出结果。不过当通道长度与当量直径之比大于100时，则可按定型流动来计算通道全长上的摩擦压降，而不再单独考虑进口段长度的问题，由此所引起的误差不会很大。