在饱和沸腾的初期，传热与在壁面附近所形成气泡的情况密切相关。在核化开始后，其成为主导的传热因素。因此所开发的预测沸腾起始热流密度的关联式在本区域仍适用。因此过冷核态沸腾和低干度饱和沸腾的热流密度是相等的。然而，当干度增高后，因为蒸发和液滴夹带导致液膜变薄，从液膜向汽芯的蒸发变得更高效，从而导致液膜内的核化被抑制，蒸发主要发生在液膜和蒸汽的界面上。大多预测环状流换热系数的关联式都是经验关联式。

在饱和沸腾区域的两相传热可以表达为如下模型：

因为主流处于饱和条件下。两相换热系数h2φ通常表达为核态沸腾传热项hNB和对流传热项hc：

不少的研究者采用该两项式的方法将其与同质量流速下全液相的换热系数相比乘以一个参数，即

式中 a1，a2，b——经验常数，各种关联式的值总结在表3-5中。

表3-5　式（3-60）中饱和流动沸腾传热系数关联式的各常数

*：关联式只在环状流区域有效，因此a1=0

Martinelli参数Xtt可以用如下关系式确定：

有两个在水的核态沸腾区域比较常用的简化关系式为Jens-Lottes和Thom关系式，它们分别表达为

和

式中，q″单位为MW/m2，p为MPa，T为℃。需要说明的是，Thom关联式的低斜率是因为他使用了早期常规锅炉的沸腾曲线的数据局限所导致。(www.daowen.com)

一个应用广泛的覆盖全部饱和沸腾区域的关联式是Chen提出的。他的关系式形式也是采用式（3-59）的形式。其对流换热部分的hc是通过修正Dittus-Boelter关系式得到的：

式中的F因子（雷诺数因子或湍流强化因子）表达了因为气泡存在所引起的湍流强化效应。

图3-12　Chen关联式中所用到的雷诺数因子F

F可以采用如图3-12所示的图形化方法确定。也可以用式（3-65）近似得到：

图3-13　Chen关联式的抑制因子S

而核态沸腾部分则基于Forster-Zuber关联式，采用S因子（抑制因子）修正：

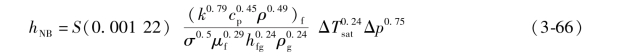
式中，ΔTsat=Tw-Tsat，Δp=p（Tw）-p（Tsat）；抑制因子S是总雷诺数的函数，示于图3-13中，可以近似为：

式中，Re=RefF1.25。原始数据的参数范围为：p=0.17～3.5 MPa，液体入口速度为0.06～4.5 m/s，热流密度最高到2.4 MW/m2，干度x=0～0.7。其他所测试的流体包括甲醇、环己烷、戊烷、苯等。

Chen关联式的优势在于其涵盖了整个沸腾区域。其误差（11%）比更早的所发表的各种关联式低。后来的数据又延伸到压强为6.9 MPa的条件下，这已经覆盖蒸汽发生器的工况范围。因此，到目前为止，Chen关联式仍然是工程上主要使用的一个关联式。

Collier用温度修正讨论了将Chen关联式延伸到过冷区域的可能性：

q″=hNB(Tw-Tsat)+hc(Tw-Tb)　(3-68)

对于过冷沸腾，F因子可以设为1，S可以按照x=0来计算。该方法在预测水和氨等的实验数据时吻合较好。