Bergles和Rohsenow基于Hsu和Graham的推荐开发了沸腾起始（即z=ZNB）的判据。他们的分析后来被Davis和Anderson的更通用的推导所证实。主要的前提是壁面附近的液体因为加热，其温度必须等于使气泡稳定的过热温度（图3-10）。第一次相等发生在两条温度分布曲线相切的位置，假设壁面具有各种孔隙尺寸，气泡以初始半径r*在其中生长。液体温度和热流密度用下式关联：

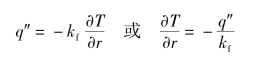
图3-10　壁面上气泡核化的临界孔隙尺寸

当孔半径等于下式时，该梯度等于核化所需的过热度[由式（3-43）给出]的梯度。

为了保证气泡核化，假设液体过热边界层延伸到临界半径的两倍厚度。根据该假设，进行适当的整理后，得到：

式中，下标i表示沸腾起始点，在沸腾起始点，热流密度也可以表达为对流定律的形式，有：

因此壁面过热度的计算式为：(www.daowen.com)

式中，

在低热流密度下，这些相切点的半径可能比壁面上最大半径的孔口还要大，式（3-46）可能会低估所需要的过热度（q″）i。Bjorg等推荐认为大部分与水接触的表面的最大空穴半径为rmax=10-6 m。如果表面润湿性很好，表观空穴尺寸要比实际尺寸小。

Rohsenow研究发现当最大空穴半径曲线与单相点曲线刚好相切时，其换热系数为：

如果换热系数hc小于这个数值，式（3-46）就不能满足。当液体温度Tb饱和时，hc的数值为kf/2rmax，与过热边界层的厚度是最大空穴半径两倍的假设一致。

对于水压力为0.1～13.6 MPa时，Bergles和Rohsenow给出了如下经验关联式：

式中，q″的单位为W/m2，p为MPa。该式假设加热表面有大量的微孔，忽略表面的粗糙度影响。按照式（3-50）所计算出的起始沸腾热流密度较低，该式是基于可视化观察所得到的结果，而不是根据表面温度响应来判定的，这需要大量的核化气泡产生才会有该效果。