对于纵掠棒束充分发展的湍流,因为棒束子通道各向强烈的不均匀性,其Nu值可能与纵掠圆管的情况有显著不同。因此Nu数和h与在棒束的位置有很大的关系。然而,当Pr>0.7之后,Nu数对边界条件就变得不这么敏感;此外,如果考虑将沿燃料棒的冷却剂湿周定义一个在外周无剪切的当量环,发现在P/D≥1.12时所预测的Nu数误差在10%以内。
通常采用的方法是在充分发展的圆管的Nu∞数计算关联式的基础上,添加一个修正因子ψ:
![]()
式中,除了特别声明以外,Nu∞ c.t.一般使用Dittus-Boelter关系式。
(1)无限栅格
对于正方形栅格,当1.05≤P/D≤1.9时,
![]()
对于三角形栅格,当1.05≤P/D≤2.2时,
![]()
在采用水作为冷却剂时,Weisman建议:
![]()
对于正方形栅格,当1.1≤P/D≤1.3时,
![]()
对于三角形栅格,当1.1≤P/D≤1.5时,
![]()
式中 P——栅距,m;
D——棒径,m。
从式(3-17)不难看出较稀疏的栅格给出较高的换热系数。
(2)有限栅格
Markoczy给出了有限栅格中任何棒的统一表达式为
![]()
式中,Re数的特征尺寸根据围绕该棒相邻子通道的水力直径来确定,![]() ,其中j代表该棒相邻的第j个子通道;指数B为B=De/D。对于正方形栅格,ψ值与实验值在概然误差为8.58%下的平均偏差为12.7%。适用条件为:3 000≤Re≤106,0.66≤Pr≤5.0,三角形栅格1≤P/D≤2.0,正方形栅格1≤P/D≤1.8。
,其中j代表该棒相邻的第j个子通道;指数B为B=De/D。对于正方形栅格,ψ值与实验值在概然误差为8.58%下的平均偏差为12.7%。适用条件为:3 000≤Re≤106,0.66≤Pr≤5.0,三角形栅格1≤P/D≤2.0,正方形栅格1≤P/D≤1.8。
(3)入口效应
在实际工程中,沿通道长度h并不是常数,主要有以下两个原因:
①在入口后一段距离,温度分布处于变化中。
②因为温度变化导致物性参数发生改变。(https://www.daowen.com)
温度对物性的影响一般采用定性温度来表征,一般采用入口和出口温度的平均值来代表。
而入口效应则要复杂得多。入口段长度一般与Re数,Pr数、热流密度曲线分布和流体的入口条件等因素有关。在入口段区域内,传热系数h从无限大急剧下降到某个渐进值(图3-1)。在这种情况下,用充分发展段的努塞尔数Nu∞来估计全长通道的平均努塞尔数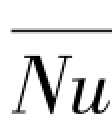 是保守的。
是保守的。
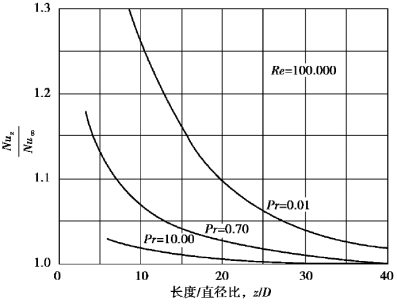
图3-1 Re=105下沿管长的局部换热系数
一般对于圆管,认为
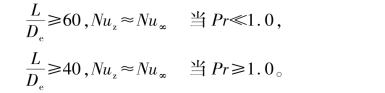
总体平均换热系数提出了几个包含有入口效应的关联式,与入口条件有关。总的来讲,入口区域的传热系数要相对高一些。
①Re>10 000,0.7<Pr<120时,对于方形入口,McAdams推荐使用式(3-19):
![]()
②对于带喇叭形入口的圆管,Latzko提出对于L/De<0.693R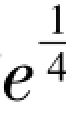 的入口段可以采用关联式:
的入口段可以采用关联式:
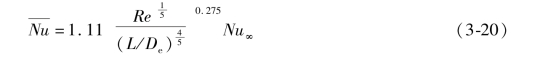
对于L/De>0.693R 的入口段,则可以采用:
的入口段,则可以采用:

式中,参数A为Re的函数:
![]()
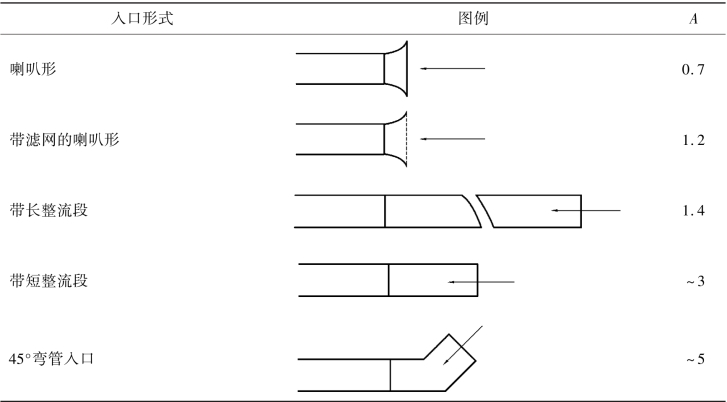
在26 000<Re<56 000区间,Latzko的预测关联式中如果采用A=1.4的预测结果要比A=1.83~2.22时要好。对气体在各种入口条件下的换热系数计算时,采用式(3-21)时的不同A值可以参考表3-3。对于过热蒸汽,可以采用如下的McAdams的推荐值:
![]()
表3-3 管内气流的努塞尔数入口系数
续表
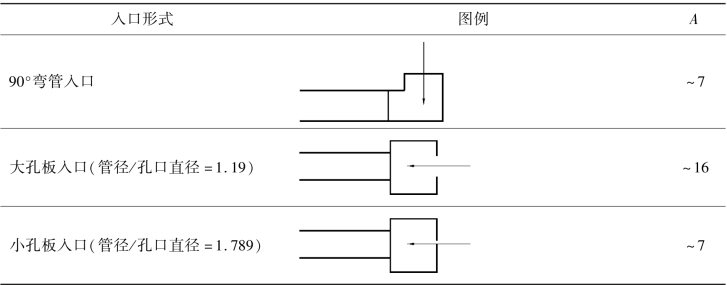
入口区域局部换热系数对于短管,充分发展段只占到很短的长度,必须考虑局部换热系数。实验给出了如下的关联式。
①入口速度和温度均匀分布条件下:

②直进口:
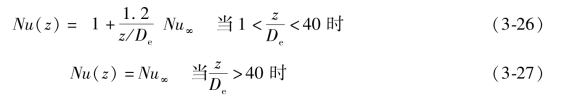
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






