在求得Tf（z）之后，可以根据对流换热方程求得Tco（z）。根据牛顿冷却公式

可得

若释热率按余弦分布，则有

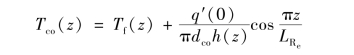
式中 dco——包壳的外径。

上式中除了h（z）外，其他参数都是已知量，所以只要确定了h（z），就可以求得Tco（z）。

假如对流换热系数h（z）沿冷却剂通道的高度变化不大，通常就可以把它作为常数处理，并采用冷却剂进出口温度的算术平均值作为计算平均换热系数h的定性温度。当z=0时，由上式可得

合并上两式，得

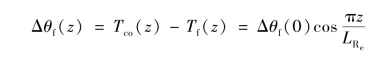
移项后有

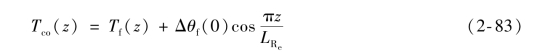
再将式（2-82）代入式（2-83）得

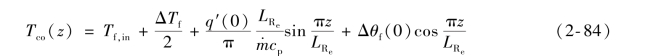(www.daowen.com)

由式（2-84）可知，Tco（z）沿高度方向是变化的。显然，在某一高度z处，Tco（z）将出现最大值。包壳外表面的最高温度Tco，max是一个很有用的量，它除了校核核燃料包壳是否达到最高许用温度外，还是估算材料的强度和判断包壳耐腐蚀的一个重要参数。例如，在压水堆中，用锆合金制造的包壳，其外表面的工作温度一般不得超过350℃，否则将会加速包壳的腐蚀。将式（2-84）对z求导数并令其等于零，就可求出当包壳外表面温度达到最大值时的位置zco，max。然后，将zco，max代入式（2-84）即可求出包壳外表面的最高温度Tco，max。求解过程如下：

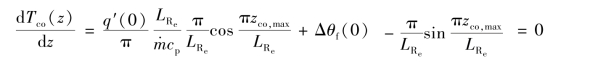
化简整理后可得

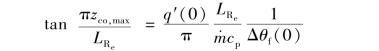
所以

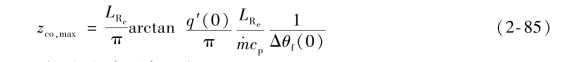
将式（2-85）代入式（2-84），则可得包壳最高温度

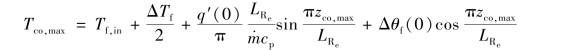
利用三角函数变换公式并利用以上几式，经简化整理得

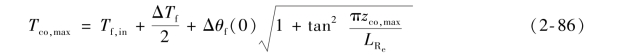
利用式（2-81）及式（2-85）化简式（2-86），则得到包壳外表面最高温度表达式为

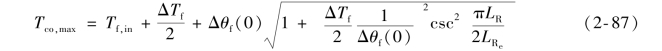
对于大型压水堆，外堆尺寸相对堆芯的高度来说是很小的。故取LR=LRe，又因为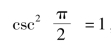，则式（2-87）可简化为

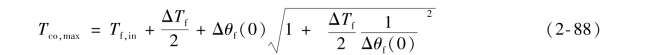
Tco（z）的分布如图2-19所示，其最大值出现在冷却剂通道的中点和出口之间。这是因为它要受两个变量的制约：一是冷却剂的温度，它沿轴向的变化与释热量分布有关，越接近通道出口，升高越慢；二是膜温差，它和线功率密度q′（z）成正比，也是沿冷却剂通道中间大，上下两端小。这两个变量的综合作用，就使得包壳外表面最高温度发生在冷却剂通道的中点和出口之间。