在导热各向同性的物质中，k是一个与材料、温度和压力有关的标量。在非各向同性的物质中，其热行为因方向不同而不同。一些高度取向性晶体类物质中，可能会有严重的各向异性。例如，沉积热解石墨与底面平行和垂直方向的热导率比可以达到200∶1。对于各向异性和非均质物质来讲，k是一个张量，在笛卡尔坐标系中可以写为

对于各向异性均质固体，该张量为对称张量，也即，kij=kji。在大多数情况下，k都可以看作为一个标量。本书也将这样来处理该物理量。

如前所述，热导率因物质不同而不同，并随着温度和压力变化而变化。k值可能从气体的接近于0到极低温下天然铜的4 000 W/（m·℃）范围内变化。

k与压力的关系因物理状态不同而不同。气相的k值与压力强烈相关，而对于固体，该效应可忽略。因此对固体来讲，热导率仅是温度的函数，也即k=k（T），可根据实验确定。对大多数金属，式（2-43）都可以在很大温度范围内得到满意的拟合结果，即：

式中，k0和β0因金属不同而不同。显然k0与参考温度T0有关。β0可能是正值也可能是负值。总的来讲，对于纯均质金属，β0为负，而对于合金则为正。

对于核燃料来讲，情况变得更为复杂，k因辐照造成化学和物理结构（燃料芯块因为温度和裂变产物变得多孔）的改变而发生改变。

即使假定k为一标量，也因为式（2-40）的非线性而难于求解。最简单克服该问题的方法是通过下述4种手段将方程转变为线性方程：

①在给定范围内k变化很小时，可以假定k为常数，这样式（2-40）就转变为

②如果在给定温度范围内k变化很大，可通过式（2-45）定义一个平均热导率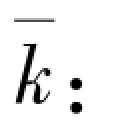

这样就可以用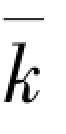代替式（2-44）中的k。

③如果对于k有经验关系式，可以得到单变量的微分方程，在大多数情况下可以转变为一个相对简单的线性微分方程。例如，式（2-43）可以写为如下形式：

因此有

则(www.daowen.com)

将式（2-48）代入式（2-40），则得到

该式是一个关于k2的线性微分方程。

④最后一个方法就是传热方程可以用下面介绍的基尔霍夫变换进行线性化。在许多情况下，可以采用如下积分：

式中 T2-T1——所关心的温度变化区间。

基尔霍夫变换主要就是通过该积分来求解修正的热传导方程。定义从T1-T的积分热导率θ为

新的变量θ可以用于如下变换：

在该式中，有

则有

在稳态下，式（2-40）变为

该方程是一个线性微分方程，可以很容易求解。

在实际应用中，核工程的计算机程序在数值求解中可以使用与温度相关的热导率。式（2-40）仍然可以在一维条件下容易求解。因此上述方法仅应用于多维问题的分析解中。