由堆物理的计算可知，单位体积的裂变率为

式中 φ——中子注量率，中子/（cm3·s）；

σf——微观裂变截面，cm2；

N——可裂变核子的密度，核/cm3；

Σf——宏观裂变截面，cm-1。

常用材料的吸收和裂变截面数据见表2-2所列。

表2-2　热中子（0.0253eV）截面数据

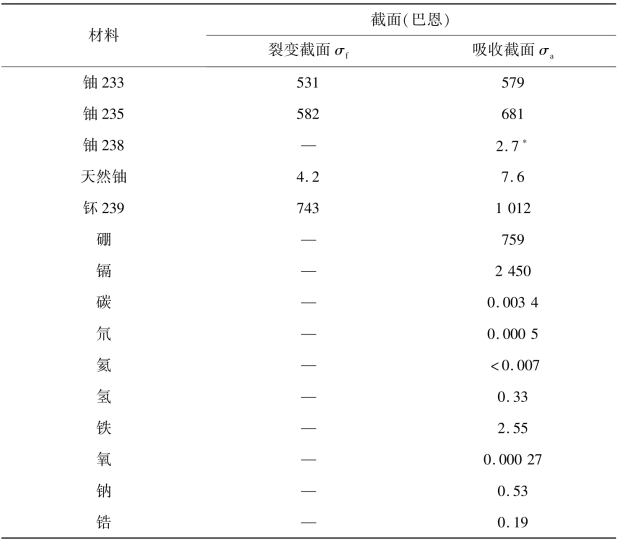
*因为超热中子的原因，典型反应堆内的238U的实际有效吸收系数比该值高。

则堆芯内单位体积的释热率q‴的表达式应为

式中 Fa——堆芯（主要是元件和慢化剂）的释热量占堆总释热量的份额。

如果堆芯的体积为Vc（m3），则整个堆芯释出的热功率Q·c为

式中 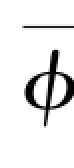——整个堆芯体积内的平均中子注量率，中子/（cm3·s）。

如果计入堆芯之外的反射层、热屏蔽等的释热量，则反应堆释出的热功率应为

或

在给定条件下，上两式的Ef、σf、Vc均为常数；式中的N是堆芯中每单位体积内可裂变燃料的核子数，如果裂变物质在堆芯内的分布是均匀的，则可认为N是常数，而实际上在运行中N是变化的。为简化起见，在分析中可认为它是常数。这样式（2-4）和式（2-6）中就只有一个变量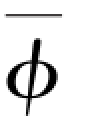了，可见堆的热功率和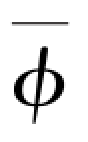成正比。此外，由式（2-3）可知，堆内的体积释热率也是与中子注量率成正比的。因而堆内热源的分布函数和中子注量率的分布函数相同。

单燃料棒参数。反应堆中有3个参数与体积释热率有关：

①燃料棒单棒功率q·。

②与传热表面相垂直的热流密度q″（可以分别按照包壳内表面、外表面或燃料芯块表面来计算，在热工计算中，以包壳外表面计算为主）。

③单位长度的功率q′（线功率密度）。

对于第n根燃料棒，这3种功率参数之间的关系为

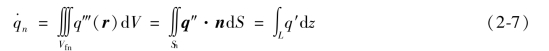
式中 Vfn——燃料元件区的释热体积；

n——包围Vfn面积Sn的外法向方向；

L——活性段长度。

根据实际需要，也可以定义如下的热流密度参数：

式中，符号{}表示面积平均值。

而平均线功率密度定义为

如果将式（2-7）应用于实际情况。对于柱状燃料元件，芯块的直径为dfo，包壳外径dco，长度为L，则燃料棒的总功率为(www.daowen.com)

如果用包壳外表面的热流密度来表示，则有

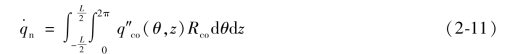
式中，忽略了元件的轴向导热及包壳和气隙中的产热。而如果用线功率密度来表示，则有

根据式（2-8），则燃料包壳外表面的热流密度为

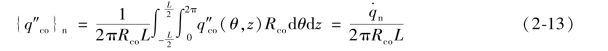
因此，对于任何一根燃料棒，有：

式中，燃料棒内平均体积释热率为

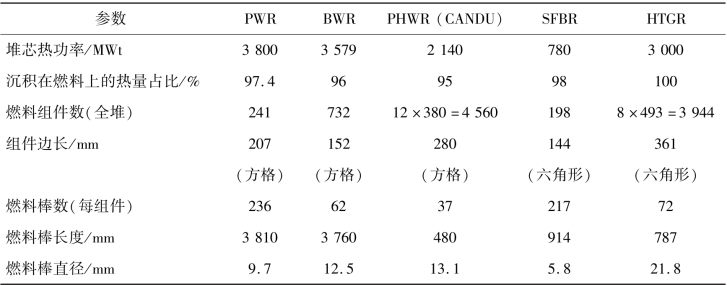
【例2-1】 各种反应堆内的传热参数。

问题：根据表2-3给出的反应堆参数，针对每种反应堆计算如下参数。

①当量堆芯直径和堆芯长度。

②堆芯平均功率密度q‴（MW/m3）。

③全堆平均线功率密度<q′>（kW/m）。

④全堆燃料棒和冷却剂间的平均热流密度。

表2-3　例2-1表

解 这里主要针对压水堆（PWR）进行求解，其他的只是给出总结果。

①当量堆芯直径和堆芯长度。

燃料组件的外表面积=（0.207 m）2=0.043（m2）

堆芯面积=（0.043 m2）×（241个燃料组件）=10.36（m2）

当量圆形直径：

堆芯长度（L）=3.81 m

堆芯总体积

②全堆的功率密度。

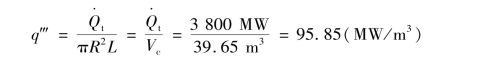
③全堆平均线功率密度。

④堆芯燃料棒和冷却剂间的平均热流密度。

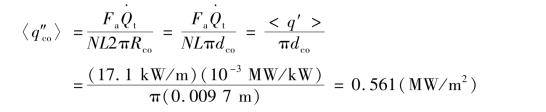
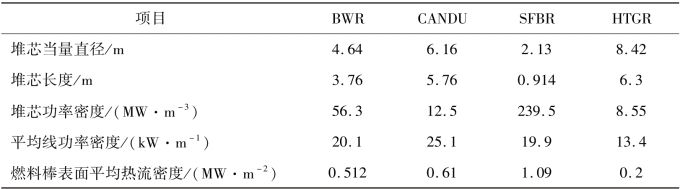
对于其他类型的反应堆计算结果见表2-4，过程就不再赘述。

表2-4　其他类型的反应堆计算结果