根据前面对情绪的分析，情绪是一个多维的系统，过去的情绪对现在的情绪有影响。而动态系统是一个和时间直接相关的多维现象。动态系统中的时间不仅仅是一个指标或一系列事件的序列。动态系统中的事件是与时间紧密相关的，未来衔接着过去，当前的行为受到过去事件的影响。前面所举的例子正说明了情绪也具有这个性质，所以用动态系统来描述情绪是恰当的。

情绪揭示的内容与生理、认知、行为、社会和文化系统等各方面都有关系，所以在相关的各个专业知识领域专家们都构建了自己的情绪定义、度量标准以及作用理论等。这样做的结果是不存在一个真正的情感科学的领域。专业化和偏见是造成情绪研究领域一些基本分歧的一个原因。另一个原因则是情绪研究一直以来都是依靠着线性的统计数据以及静态模型进行研究的。基于平均分配的统计数据，对于像情绪这样复杂的现象而言是不够发达的，并且没有足够大的模型以及预测情绪的能力。但这并不意味着它们是无用的或是没有促进情绪科学的发展，但是它们却对将情绪视为一个复杂过程的更完整的理解造成了阻碍。情绪包括了生理上的激发以及行为上的表露；它包括自我意识以及口头的表达；它具有天生固有的以及后天培养的影响力——但是所有的这些东西还是不能足以使人们了解情绪到底是什么。真正对情绪的了解和掌握来源于对情绪各个微小组成部分的大量观察，以及对它们互相作用的多次观察。下面先从线性理论来进行分析，探讨线性理论在情绪描述上的固有的局限性，同时也说明非线性理论的潜在的优越性和先进性。

1.线性理论不能确切地描述情绪的原因

在数学上，线性方程与非线性方程之间有着本质性的差别，主要表现为一个线性方程的任意两个解加在一起仍然是该方程的解，这一原理就是著名的线性方程的叠加原理。它为解决“线性”问题提供了一条思路，即可以把整个问题分解成许多个“小”问题，再把各个“小”问题的解叠加起来而得到整个问题的解，但是对于一个“非线性”问题，则不可以如此处理，因为非线性方程不再满足“叠加原理”，因此必须整体地考虑原来的问题才行。这个简单的说明告诉我们，非线性问题包含着不可忽视的复杂性。

下面从线性方程的数学角度来分析线性理论用于情绪建模的局限性。

（1）线性方程的3种基本类型 线性方程存在3种基本类型：点斜式方程、微分方程和差分方程，下面分别进行讨论。

1）点斜式方程：点斜式方程最基本的形式为

y_t=α+βx_t （9-8）

式中，y_t为因变量；α为添加的常数（或是一个扰动）；β是斜率系数，也称为回归系数；x_t是自变量。

此方程也称为一元线性回归方程，从统计学的意义上来说，是自变量每变化一个单位，因变量平均变化的单位数。

如果两个变量是线性相关的，比如受教育程度和收入，当知道一个人的受教育程度和两者的关系时，就能利用这个公式来预测收入。

简单的线性关系在心理学中是很罕有的，绝大多数现象都有复合的自变量。因此，复合的线性回归方程被研究，以使其能在复合的变量下预测结果。虽然更复杂，但这些方程仍然利用同样基本的形式：

y_t=α+β₁x₁+β₂x₂+β₃x₃+ε （9-9）

式中，y_t为因变量；α为添加的常数（或是一个扰动）；β_i（i=1，2，3）为偏回归系数；x_i（i=1，2，3）为自变量。

此方程也称为自变量数目为3的多元线性回归方程。3个自变量x₁、x₂、x₃对因变量y的影响是：①每个自变量的影响是线性的；②3个自变量影响的总体效果是简单叠加的关系（无交互效应）。

举例说明：因变量y_t表示某些人焦虑程度的值，它能被这些人的心跳频率x₁、面部恐惧表情的程度x₂、对一个害怕事物的接近度x₃，加上一个常数α和一个误差值ε来表示。可以将这个常数用来表示焦虑的基本等级，将误差值用来表示测量中的错误和没有经过测量的各种因素的集合。

2）微分方程：微分方程最基本的形式为

dy_t=α+βy_t （9-10）

式中，y_t为存在等级；dy_t为瞬时变化率。

3）差分方程：差分方程的表现形式为

差分方程描述的是在一段给定时期内变量离散的变化。(www.daowen.com)

（2）线性方程不能完整地构建情绪模型的原因

1）对于点斜式方程：对于单变量的点斜式方程来说，如果情绪能够被定义为一个单一变量的系统，那么这些方程就能很好地构建情绪的模型。但是现在并不存在一个一致的情绪的度量尺度。人们可以说血压是142/95，也可以说扁桃体的活性增加了20%，但是不能说某人的焦虑等级为12。尽管情感计算有很多检测人体情感信息信号的方法，但是到目前为止，还没有人能把一致的度量标准放在一起组成一个简单的检测，而这种检测对于点斜式方程是必要的。

多重回归对情绪度量的设计可能是有帮助的，能比较和结合多个变量（例如面部特定肌肉的紧张度、血压、血浆中的肾上腺素、扁桃体活性等），以此来发展一个回归方程，使其能够在一个特别的时刻及时地产生一个单一的情感的测量值。但是在一个单独时刻描述一个情绪时，有效性总会受到限制——相比之下，了解或预测它下一次会出现怎样的情绪或是单独的组成部分是怎样互相作用的，则更为困难。最好的是线性回归能表现出情绪的一个组成部分（如恐惧思想），它是和其他部分（血压和行为）相关的。但是当这种使人感兴趣的现象变为一个复杂系统时，线性回归的逻辑就变为循环的了：自我报告预测血压，而血压预测面部情绪，面部情绪预测对恐惧事物的接近度，而这个接近度又预测自我汇报，以此类推。因此，虽然线性方程可以在系统的各个部分建模中使用，但是线性方程不能为整个情绪系统建模。

2）对于差分方程和微分方程：差分方程优于点斜式方程的地方是，前者能模拟一个变量随时间的变化；微分方程也是类似的，但在实际应用中，只有离散的差分方程才可以计算。下面举一个简单的例子，说明为什么简单的差分方程和微分方程不能准确地模拟情绪的复杂性。

y′-0.5y=0 （9-12）

y″+y=0 （9-13）

y″+0.5y+y=0 （9-14）

方程式（9-12）的解是

y₁（t）=0.25e^0.5t （9-15）

方程式（9-13）的解是

y₂（t）=0.5sint+2cost （9-16）

方程式（9-14）的解是

y₃（t）=0.5e^-0.25t[cos（0.968×0.25t）+2sin（0.968×0.25t）] （9-17）

这3个方程式的解的曲线如图9-7所示。

从图9-7中可以看到，情绪不会具有式（9-15）所描述的无限的指数级增长的特性，情绪也不像式（9-16）所显示的是无衰减的反应，它有清楚的内部与外部压力去规则和限制情绪的反应。在以上3个公式中，式（9-17）可能是最接近模拟情绪反应波形的，但情绪不具有一个规则振动的固定周期、振幅和频率。如果它有的话，预测情绪反应将是一个相对简单的任务。因此，简单的差分方程和微分方程都不能准确地模拟情绪的复杂性。

总之，情绪是包括时间变化和不能被线性准确描述的复杂现象。

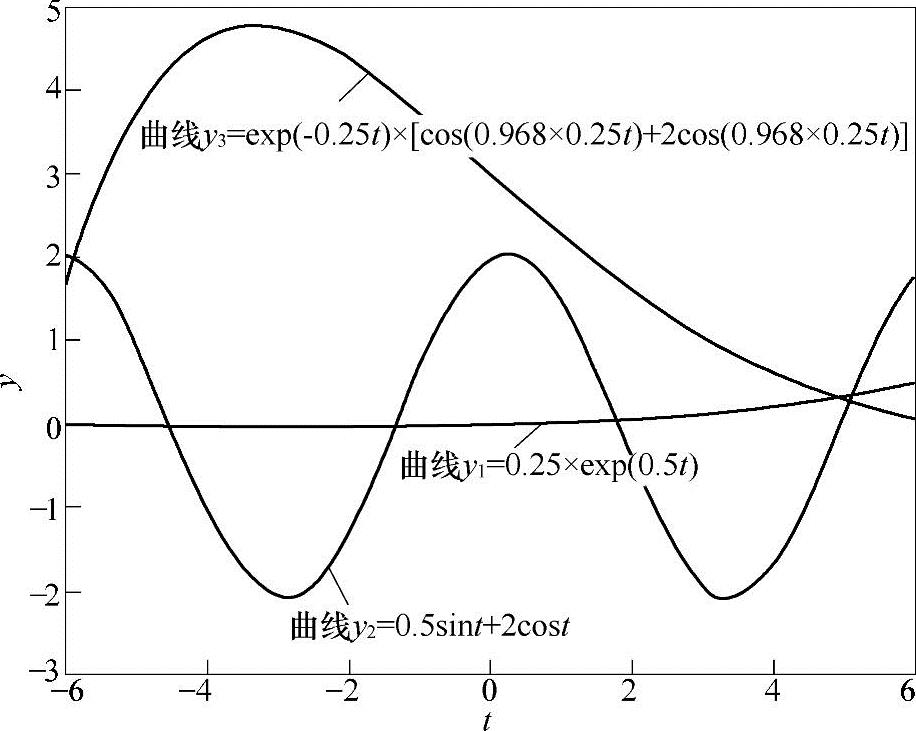
图9-7 3个微分方程的解

2.非线性理论在情绪建模研究中的优越性

在某种定义上，非线性科学是研究复杂性的科学，这句话这样理解比较贴切：非线性科学有可能使现实世界中那些杂乱无章的空间形态和似乎毫无规律的时间序列成为研究对象，并从中发现它们的“复杂”规律性。而情绪正是一种对初值敏感、动态变化的复杂现象。非线性动态系统分析具有描述和模拟复杂现象的能力，在情绪研究中应用非线性动态方程可解答大量的问题。