可以在机器中实现情感模型的构造存在着两种途径：其一是直接模拟人的神经系统的构造与活动特性，这是最本质的模拟，但由于人对脑的认识局限性和计算机运算能力的限制，在目前是难以实现的；其二就是从情感活动结果的特点出发，有限度地去模拟人或动物的基本情感，以获得具有机器人特有的情感行为，实现和谐人机交互，本书选用此法。

著名的西米诺夫提出了有机体的信息与情绪之间的关系，他的理论直接表现为信息理论。我们从信息的角度出发可以构建机器的情感模型为

E=-N（I_n-I_a） （9-2）

式中，E为机器情绪；N为需要系数，受生理需要、安全需要控制，它们直接影响机器对信息的敏感度，N将随着机器的虚拟生理需要、安全需要不断发生变化，需要系数N等于生理需要因子N_p和安全需要因子N_s权重的和，即N=（N_p⊕N_s）；I_n为需要信息，指机器和人在交互过程中机器期望获得的信息；I_a为所得信息，指机器和人在交互过程中机器所获得的信息。

按照这个公式，信息按一定形式进行交流便可达到目的。因此，如果机器因缺乏信息而不能适当地组织自己，那么就会使消极的情绪开始行动。但是，如果信息过剩，信息为机器所感兴趣的内容，积极的情绪便会产生。按照公式，I_a＞I_n，即所得信息超过需要信息。

机器的情绪生成是与其情感信息需求及其满足程度直接相关的。机器的期望获得的信息和所获得的信息是多层次的，属于多目标问题。对于多目标问题，各目标的重要程度不同，决策者对目标重要程度所进行的比较及量化称为“价值权衡”，价值权衡最终体现在各个目标的“加权系数”的赋值上，或体现在“影子价格”或决策者为实现某一目标所“愿意支付的代价”上。上述价值权衡、加权系数、影子价格和愿意支付的代价这4个概念是同一本质的。通过引入权重系数的概念就可以对I进行归一量化。

确定权重系数的实用方法——层次分析法：

1.问题的提出

层次分析法是美国运筹学家沙旦提出来的，是一种定性与定量相结合的多目标决策分析方法，力求将决策者的经验判断给予量化。

2.原理

设n个物体A₁、A₂、…、A_n的重量分别为w₁、w₂、…、w_n，两两比较重量，得比值矩阵A。

用重量向量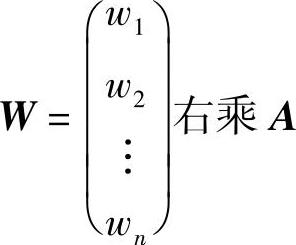

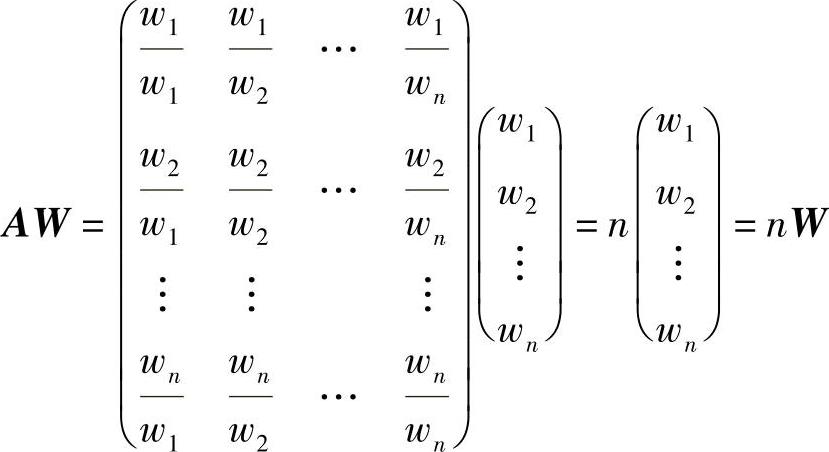
可见：1）W为特征向量；n为特征根。

2）A有如下特点：

①a_ii=1（a_ij为矩阵A中第i行，第j列的元素）；

②a_ij=1/a_ji；

③a_ik=a_ija_jk；

④A具有唯一非零的最大特征根n。

若判断矩阵具有上述特征，则该矩阵具有完全一致性，而人为的判断总会有误差。

3.步骤

1）建立层次结构模型。

2）构造判断矩阵：决策者对多个属性的重要程度作比较，同时进行比较和判断的属性不能过多，实验表明，不能超过7个因素。

“两两比较法”是每次在n个属性中只对两个属性进行比较，对i、j两个因素进行比较时，作如下约定：

和决策者对话，进行两两因素之间重要程度的比较，有如下结果：

根据上述对话结果，得到比较矩阵A：A=|a_ij|_n×n

矩阵A具有如下性质：

1）a_ij=1

2）

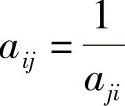
根据上述性质，和决策者对话进行两两比较的次数不是n²次，而是n（n-1）/2次。

3）求矩阵A最大特征根λ_max，然后求出相应的规范化的特征向量W，即

AW=λ_maxW

对于其中的各分量就是对应于各因素的权重系数。

4）一致性检验：用两两比较法和决策者对话可得到比较矩阵，但是可能会发生判断不一致，所以需要进行一致性检验。一致性检验，就是检查决策者对多属性评价的一致性。完全一致时，应该存在如下关系：

a_ik=a_ija_jk

反之，就是不一致。由于不一致性在所难免，那么存在多大的不一致性是可以被接受的呢？这就是一致性检验所要讨论的内容。

一致性检验：当判别不一致时，一般λ_max≥n，此时

λ_max+∑λ_i=∑a_ii=n

λ_max-n=-∑λ_i

为检验判断矩阵一致性，定义一致性指标为

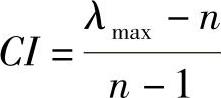
1）当λ_max=n，CI=0，为完全一致。

CI值越大，判断矩阵的一致性越差。

2）一般，CI≤0.1认为可以接受。(www.daowen.com)

维数n越大，一致性越差，引入修正值CR：

Saaty构造了最不一致的情况，就是对不同n的比较矩阵中的元素，采取1/9、1/7、…、1、…、7、9随机取数的方式赋值，并且对不同n用了100～500个子样，计算其一致性指标，再求得平均值，记为RI，结果见表9-1。

表9-1 一致性指标平均值

取CR=CI/RI作为更合理的检验判断矩阵一致性指标，只要满足CR≤0.1，就认为所得比较矩阵的判断可以接受。

4.常用的简便计算方法

上述计算权重系数的方法比较麻烦，还有近似算法可以简便地计算权重系数，下面介绍两种常用方法。

（1）和积法 这种方法的步骤如下：

1）对A按列规范化

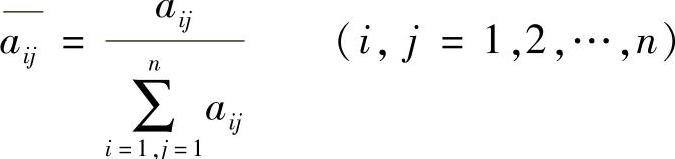
2）再按行相加得和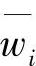

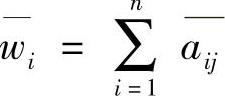
3）再规范化，即得权重系数w_i

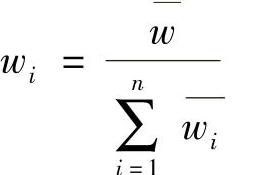
（2）方根法 这种方法的步骤如下：

1）按行元素求积，再求1/n次幂，得

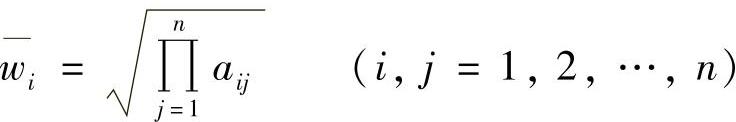
2）规范化，即得权重系数w_i

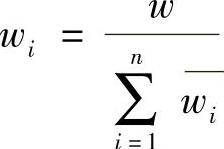
5.建模

假设机器的需求分别为x₁、x₂、x₃、x₄。其中，x₁为归属与爱的需求（多指渴望得到用户的认同、接受，与用户建立良好和谐的人际关系），x₂为自尊的需求（多指希望自己能够胜任所担负的工作，希望得到用户的高度评价，自尊需要的满足将产生自信、有价值和“天生我才必有用”等的感受），x₃为认知需求（机器渴望了解用户的信息，或从用户处学到新的知识），x₄为自我实现欲望（多指机器对于自我发挥和完成的欲望）。在建模中，权重系数完全取决于设计者对机器的性格要求，不同的设计者所得到的权重系数不尽相同。在个性化建模时，与设计者或用户对话的结果是：

1）x₁与x₂相比，两者重要性差不多，所以a₁₂=1；

2）x₁与x₃相比，x₁重要，所以a₁₃=5；

3）x₁与x₄相比，x₁重要得多，所以a₁₄=7；

4）x₂与x₃相比，x₂重要，所以a₂₃=5；

5）x₂与x₄相比，x₂重要得多，所以a₂₄=7；

6）x₃与x₄相比，x₃稍重要，所以a₃₄=3。

得比较矩阵A为

用“和积法”计算权重系数，得

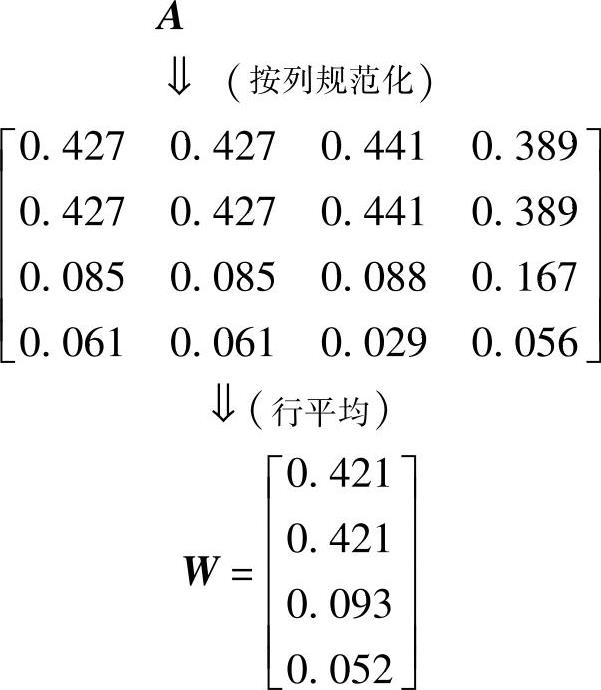
通过计算，各w_i值达到小数点后3位，由于和决策者对话显然达不到如此高的精度，因此取到小数点后两位已经足够了，所以权重系数可取为w₁=0.42、w₂=0.42、w₃=0.1、w₄=0.05。

最大特征根的简易算法是：

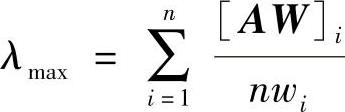
对上例中的λ_max计算如下：

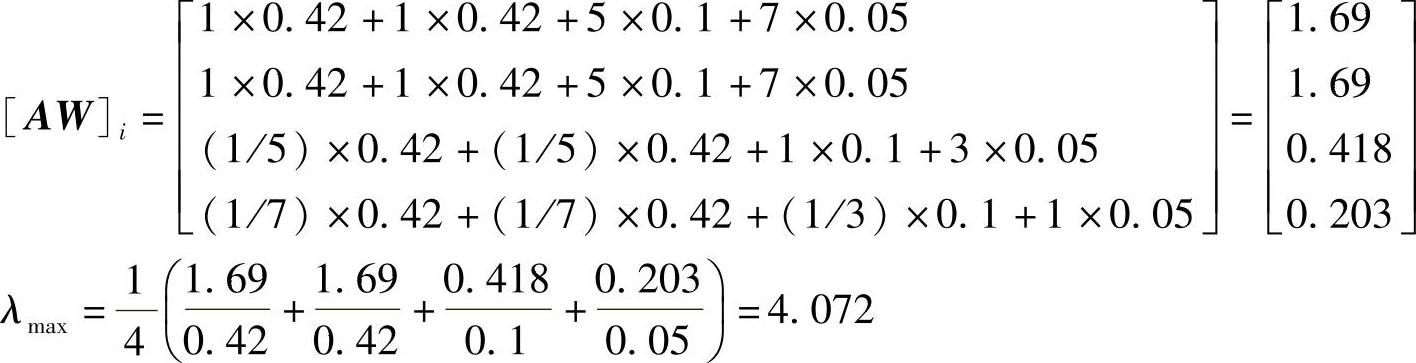
计算CI得

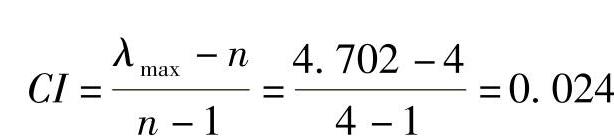
查n=4时，CI=0.9，计算得

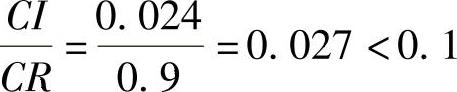
所以与用户对话所得结果的不一致性可以被接受。求得的权重系数w_i可以使用，即

I=w₁x₁+w₂x₂+w₃x₃+w₄x₄=0.42x₁+0.42x₂+0.1x₃+0.05x₄ （9-3）

这样，就可以得到归一化的I了。对于设计一个特定性格的机器来说，它的信息归一化的权重系数w是固定不变的。在某一个具体交互主题下，通过初始化x₁、x₂、x₃、x₄，就可以得到机器在交互过程中期望获得的信息I_n，即

I_n=w₁x₁+w₂x₂+w₃x₃+w₄x₄ （9-4）

在实际机器和人的交互过程中，机器从每句对话或某几句关联的对话所获得的信息是不同的，通过计算他们的评价值x₁′、x₂′、x₃′、x₄′的权重和，就可以得到机器和人在交互过程中机器所获得的信息I_a，即

I_a=w₁x₁′+w₂x₂′+w₃x₃′+w₄x₄′ （9-5）