如表7-6所示，分别选择了最具有代表性的，并且对表情的变化起主导作用的12组AU来作为合成人脸面部表情的12个基本单元。每一个AU控制了不同的节点，例如AU1控制的节点有4个，分别为17、50、15、48；而AU9控制的节点有19个，分别为5、25、58、26、59、33、66、16、49、17、50、18、51、22、55、68、70、72、74。每个节点的坐标见表7-5。每一个键盘上的键都可以控制一个AU，例如1键控制AU1，2键控制AU2，3键控制AU16。

表7-6 AU和所对应的节点

在确定好需要控制的AU后，要统计代表AU运动的运动向量所包含的节点在每一种情绪所对应的表情中，相对于初始状态（即没有表情的状态下）的位置变化。根据参考文献[22]中所述的分类和统计方法，可以将AU与FAP的对应关系进行归纳总结。这里，不再赘述每一个相关列表中的详细内容，仅列举其中的几项来说明面部表情运动计算的过程。

如前所述，FACS在很大程度上影响了表情分析领域内的研究。这个系统可以将可见的面部运动通过解剖学的原理进行分析。在FACS中，使用AU来作为度量单位。一个AU可以将几束肌肉运动结合起来。MPEG-4FAP与FACS的关系也很是相辅相成的。如表7-7所示，每个AU都对应着一到多个FAP。

表7-7 FAP到AU的映射关系

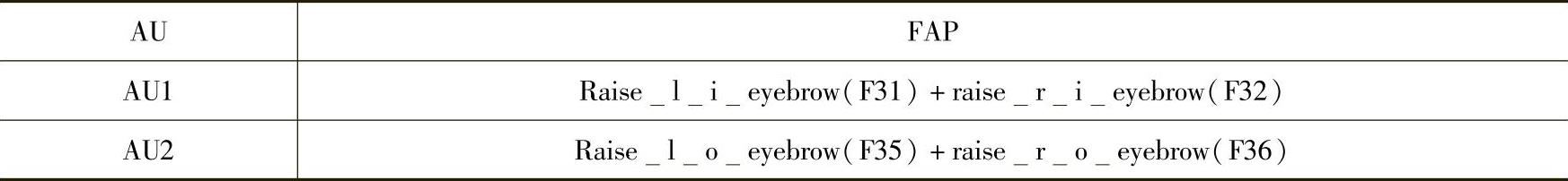
通过分析表情对应于AU的关系，可以找出情绪和FAP之间的对应关系，见表7-8。

表7-8 情绪所对应的FAP描述

通过描述脸部区域相关点的运动来度量实际图像中的FAP。如表7-9所示，这种方法为表情分析和动画合成提供了很好的桥梁作用。

表7-9 FAP的变量模型

(www.daowen.com)

根据参考文献[22]，通过前人在该领域中的研究，可以获得每一个FAP对应于不同情感状态下的平均值和标准方差值，见表7-10。

表7-10 FAP的统计数据

表7-10中，“-”表示统计数据还不完整。计算FAP每个变量变化范围的步骤如下：

定义m_i，j和s_i，j分别代表FAP中每个F_j的平均值和标准方差，则每个F_j的变化范围X_i，j可以由下式得到：

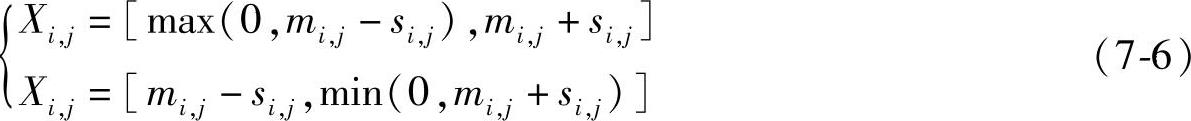
最终的变化值见表7-11。

表7-11 情绪所对应的FAP变化范围

最后要实现的功能是针对特别选取的AU，即那些对于表情变换起到特定作用的AU，通过改变其量值，从而控制其对应的FAP，在各自的变化范围内进行运动。通过键盘控制AU，当每个AU向量的运动超出了允许范围时，其对应的节点会重新回到初始状态的位置，在达到在理论上可以合成任意表情的功能，并可以沿X、Y、Z轴进行任意角度的旋转，如图7-25所示。

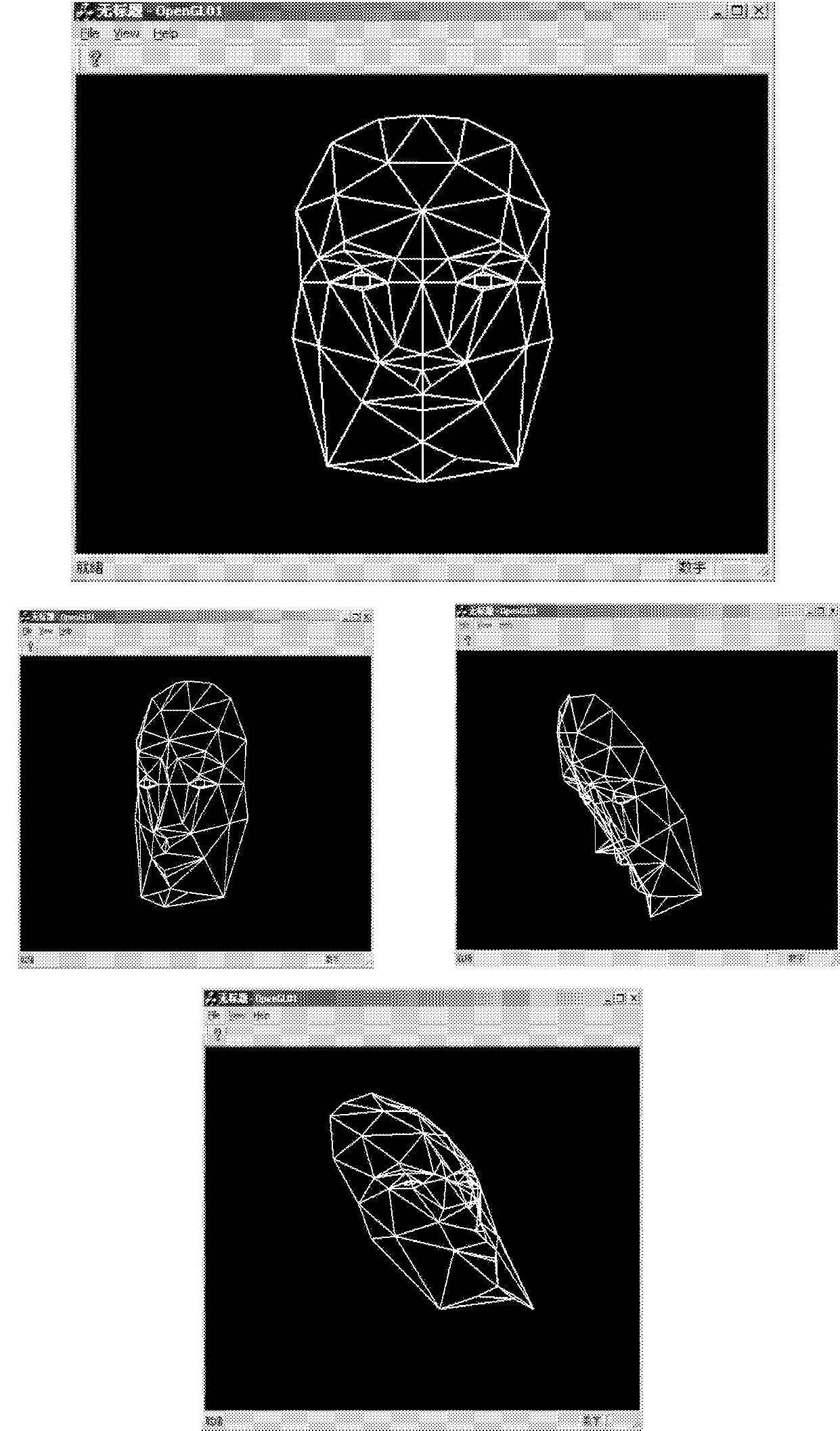
图7-25 面部表情的运动计算结果