人工神经网络（Artificial Neural Network，ANN）是在人类对其大脑神经网络认识理解的基础上，人工构造的、能够实现某种功能的神经网络，它是理论化的人脑神经网络的数学模型，是基于模仿大脑神经网络结构和功能而建立的一种非算法的信息处理系统。人工神经网络吸取了生物神经网络的许多优点，因而有其固有的特点：

（1）高度并行性 人工神经网络是由许多相同的简单处理单元并联组合而成的，使其对信息的处理能力、效果惊人。

（2）高度非线性全局作用 人工神经网络的每个神经元接受大量其他神经元的输入，并通过并行网络产生输出来影响其他神经元。网络之间的这种相互制约和相互影响，实现了从输入状态到输出状态空间的非线性映射。从全局的观点来看，网络整体性能不是网络局部性能的简单叠加，而表现出某种集体性的行为。

（3）良好的容错性与联想记忆功能 人工神经网络通过自身的网络结构实现了对信息的记忆，而所记忆的信息存储在神经元之间的权值中。从单个权值中看不出所存储的信息内容，因而是分布式的存储方式，这使得网络具有良好的容错性，既能进行模式信息处理工作，又能进行模式联想等模式信息处理工作，还能进行模式识别工作。

（4）十分强的自适应、自学习功能 人工神经网络可以通过训练和学习来获得网络的权值与结构，呈现出很强的自学习能力和对环境的适应能力。

1.带有偏差单元的递归神经网络

针对人工神经网络中，传统BP算法采用普遍的梯度下降法存在容易陷入局部极小点、收敛速度慢等缺点，带有偏差单元的递归神经网络是在BP网络的基础上，加入反馈信号及偏差单元，增加网络本身处理动态信息的能力，利用网络的内部状态反馈来描述系统的非线性动力学行为的。由于这一网络结构的特点，尤其是其在学习过程中便于引入经验知识（在偏差的选择上，可以采用模糊知识概念），大大提高了学习速度；同时，网络的隐层节点输出和输入之间有一个延时的反馈，能够储存过去的输入输出信息，它不仅可以学习空间序列模型，还可以学习时间序列模型，因此带有偏差单元的递归神经网络能够反映人对服装感性评价序列中的非线性特征。

带有偏差单元的递归神经网络由三层节点构成：输入层节点、隐层节点和输出层节点，两个偏差节点分别被加在隐层和输出层上，隐层节点不仅接收来自输入层的信号，还接收隐层节点自身的一步延时输出信号，因此隐层节点称为关联节点。其总体拓扑结构如图6-23所示。

图6-23 带有偏差单元的递归 神经网络的拓扑结构

网络学习的具体算法步骤如下所述：

1）设置允许误差ε、隐层节点数n与样本总数N，初始化网络的权值和阈值。

2）依次算出各层的输出，如下列各式所示：

式中，C_j（k）为带有偏差单元的递归神经网络的输出层单元的响应；y_j（k）为带有偏差单元的递归神经网络的输出层单元的输入；x_i（k）为第i个隐层节点的输出；σ（·）为隐层节点的非线性激活函数；S_j（k）为第j个隐层节点的输入；WI为从输入层到隐层的权系数；WR为回归信号的权系数；WO为从隐层到输出层的权系数；WI_jbias为加在隐层上的偏差单元的权系数；WO_bias为加在输出层上的偏差单元的权系数；NH为隐层节点数（除偏差节点）；NI为输入节点数（除偏差节点）；I_m（k）为带有偏差单元的递归神经网络在时间k的第m个输入。

3）计算各层误差信号，如下列各式所示：

式中，D_j（k）为输出层各单元的一般化误差；E_i（k）为中间层各单元的一般化误差；T为希望输出。

4）调整权系数及阈值，如下列各式所示：

式中，α为输出层权值的学习速度；β为隐层权值的学习速度；γ为递归层权值的学习速度。

5）修改各层偏置值，如下列各式所示：

式中，λ、μ为要求的偏差值；v为输出偏置单元的学习速度；κ为输入偏置单元的学习速度。

步骤2）～5）反复执行，直到全部m个模式对训练完毕，输入下一组样本，学习样本结束后，更新学习次数，如果误差满足要求，学习结束。

2.算法的设计与实现

搭建一个可用的人工神经网络，首先涉及并且一直贯穿整个设计过程的，就是对网络结构的设定和参数的调整。经过实验过程中的不断调试和积累经验，最终得到了一个在性能和效果上较为令人满意的网络结构。结构选定与调整过程如下所述：

1）考虑到网络复杂程度和需要调节的参数数量，决定选用三层网络。通过衡量、比较网络收敛速度和学习精度，将中间隐层和相应的误差反馈层节点均设为9个。

2）此实验是对人的喜好程度的模拟追踪实验，人类喜好的数字化结果往往是在一定范围内波动，而不能像可测量的数据一样精确到某一具体数值，如顾客这次给出的喜好的评价值为2.1，下次再评价时虽然是相同的感觉，却不一定能够给出2.1，也许是2.2，也许是1.9。考虑到这一点，本实验将网络学习的最大误差级设定得略低了一些（低0.05）。另外，在不断地调整实验中也证明了，略微提高一下允许的误差值对于网络的稳定也是有一定帮助的。

3）网络中需要调节的部分包括一些经验参数和网络各层的函数，总计16个。经验参数和各层函数都是在一次次实验过程中分析、比较得到的。由于参数过多，并且对于不同训练样本所作的设定是不同的，因此本节中就不一一例举，请参见程序。这里仅指出各层的函数（总计4个）设置：输入层到隐层间的函数和隐层到输出层间的函数如式（6-34）所示。输出层单元的一般化误差函数如式（6-35）所示，隐层单元的一般化误差函数如式（6-36）所示（其中“.”运算符代表矩阵中元素的运算）。

X=1./（1.-e^-S） （6-34）

3.实验与结果分析

为了验证模型的有效性，首先创建了包含141张服装图片的特征库，其中包括春秋装42套、夏装59套、冬装40套。每个季节选取8套（共24套）具有代表性的服装作为实验和评价的样本。在校内选取男女比例为1∶1，共20名同学进行对24套样本服装的评价收集活动，最后进行均值处理，得到实验所用的样本评价值。

将表示服装特征的一维数组作为神经网络模型的输入值。网络输出，即网络学习的目标，设定为对相应服装的评价值。

由于我们引入了不同季节的服装，因此增加了实验的复杂程度，按照需要将实验分为四组，如下所述：

1）测试、分析网络学习速度和学习效果，并与原先研究所使用的方法进行比较。(www.daowen.com)

2）对相同季节服装进行预测（测试、分析网络的预测效果），与原先研究所使用的方法进行比较。

3）对相近季节服装进行预测（测试、分析网络的预测效果）。

4）对相反季节服装进行预测（测试、分析网络的预测效果）。

如果所有实验均取得成功，便可以通过记载用户先前的心理模型，在其他季节到来时推算出用户喜好的不同季节的服装，从而使用户摆脱在不同时间段一次次评价样本服装、重构心理模型所带来的疲劳，为使用者构造出更加人性化的智能导购空间。

（1）实验1及分析 经过上节中所述的网络调整过程后，得到了一个基本稳定的带有偏差单元的递归神经网，网络性能良好，在学习过程中能较快收敛，将误差值控制在设定值之内。收敛步数及学习效果如图6-24所示。

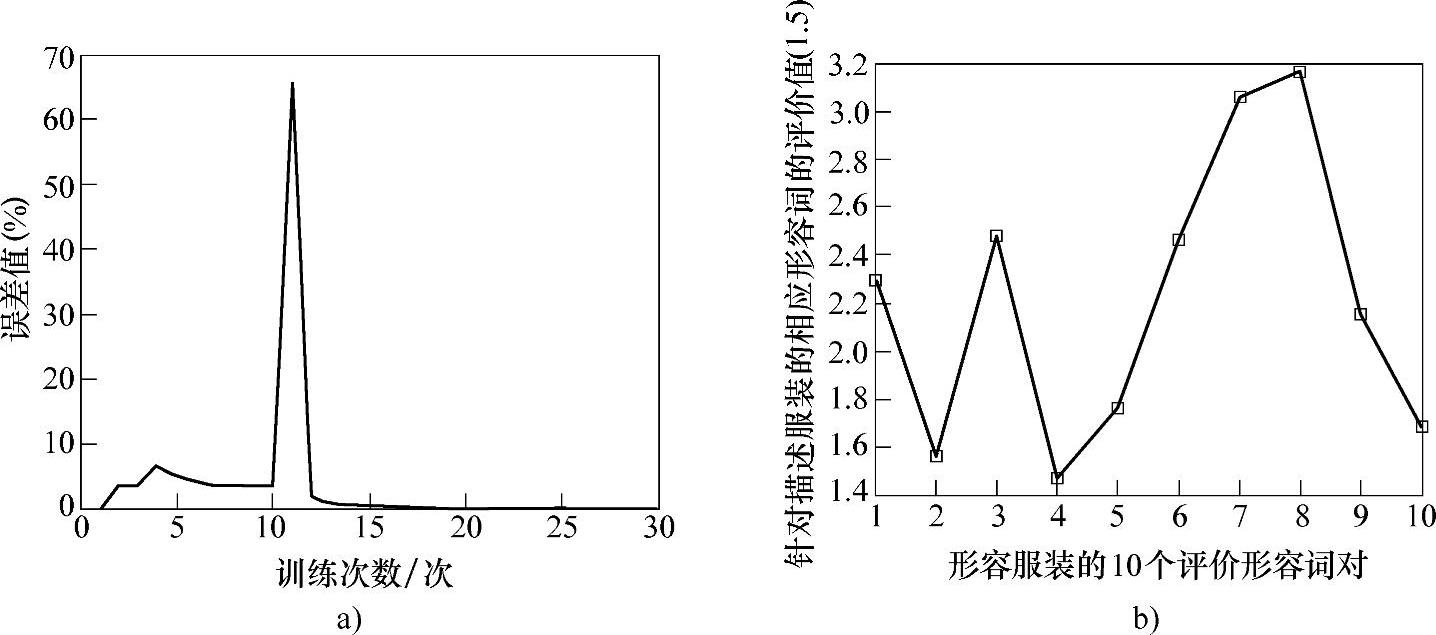
图6-24 曲线收敛情况和学习效果

a）网络学习收敛步数 b）带有偏差单元的递归神经网络对服装评价的学习效果

如图6-24所示，使用此方法的神经网络只需循环30次即可达到要求的学习效果：最大误差e＜0.05。并且平均用时小于2s，完全能够达到网络所需的实时计算要求。下面就学习时间和收敛步数与原先研究中使用的IGA进行比较，见表6-7。

表6-7 与原先研究方法的比较

经过客观的研究与分析，使用带有偏差单元的递归神经网络进行学习使用的时间从表面上看虽然比使用IGA要快得很多，但若对两者的使用方式进行比较就可以得到原因，并且可以得到更深一步的结论：

IGA算法在每次循环过程中需要与用户进行交互，询问用户的意见，以便进行下一步操作的判断，这是其费时的主要原因。而使用带有偏差单元的递归神经网络只有机器在独自计算，自然会节省很多时间。反复地询问也会给用户评定带来疲劳与压力，并且不利于在网络这种本身就有交互延迟的平台上运行，会带来更大的时间差感，但同时它也能带来一项益处——实时监测用户的感受。因此客观地讲，就学习速度这一点，带有偏差单元的递归神经网络会有很大优势，但若从用户满意度或预测的准确性来看，IGA会略胜一筹。具体差距所在将在实验2中进行分析。

（2）实验2及分析 从此实验起，将进行实际预测效果的评测，即使用学习完毕的网络对非学习样本服装进行评价值的预测，观测其预测效果。在本实验中，首先选用同季节的16套样本服装进行预测，就是令网络学习用的样本服装同预测的服装为相同季节服装。由于原先的研究大体上是在同一季节上进行的，这样规定的目的在于和原先研究建立相同的数据环境，以便进行比较分析，同时也为下一步的研究、探索打下基础。

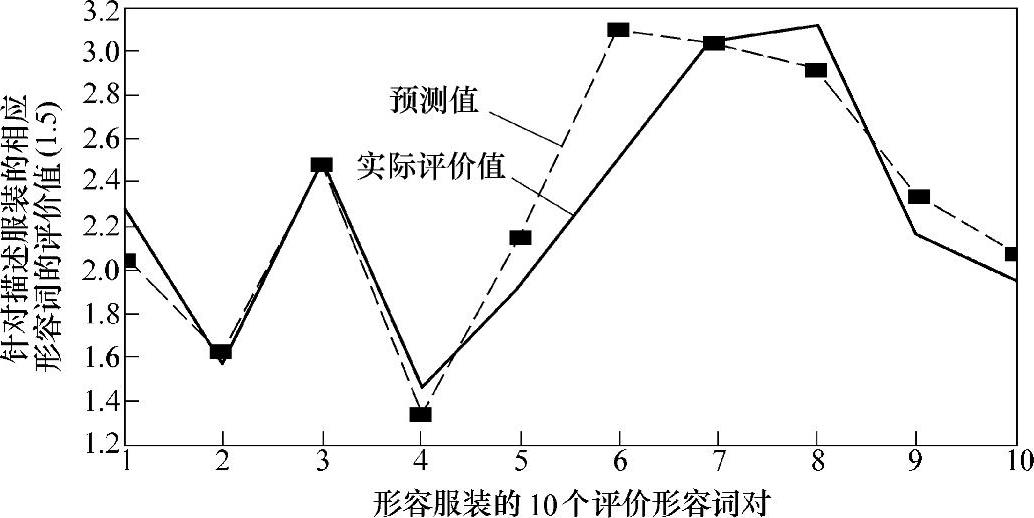
图6-25 带有偏差单元的递归神经网络对服装评价的预测效果

将希望预测的服装特征值作为学习完毕网络的输入值，即可得到此服装评价值的预测值。任意抽取某一样本，其相应的10个评价值预测结果如图6-25所示，其中，实线为实际的评价值，虚线为网络输出的预测值。

由图6-25可知，总体上看，带有偏差单元的递归神经网络可以基本模仿人对一套服装在各方面的看法走势（针对所制定的10个形容词对）。但在实验中也有出现较大偏差的时候，如图中对第6个形容词对——“粗俗的—优雅的”的预测上就出现了相对略大偏差（约0.6），可以认为，这是由于个人的评价域值不同所导致的。这样的误差还是可以接受的，并且从总体来看，预测效果还是较令人满意的。

下面，再来看一下以16个样本作为整体，对于某一形容词对的预测效果。这里为了能够与原先研究使用的方法进行比较，也同样抽取了“华丽的—质朴的”作为预测效果的研究对象，如图6-26所示。其中图a为采用带有偏差单元的递归神经网络进行预测的效果（图中实线为实际的评价值，虚线为网络输出的预测值），图b为原先使用的IGA和数量化Ⅰ类公式结合的方法的预测效果（图中粗线为实际评价值，细线为算法预测值）。

图6-26 对多个样本针对同一形容词对评价的预测效果

a）带有偏差单元的递归神经网络的预测效果 b）IGA和数量化Ⅰ类公式结合方法的预测效果

在比较中可以看出，IGA的确比带有偏差单元的递归神经网络更能准确地预测用户的评价，验证了上一节中得出的推论。但从预测情况上看，带有偏差单元的递归神经网络也基本上能够跟踪用户对不同样本给出不同评价的走势，并且考虑到其更能满足网络的实时性要求的性能，因此可以认为这种算法还是比较满足使用要求的。

（3）实验3、实验4及分析 作为预测的拓展研究，按照循序渐进原理，首先进行实验3相邻季度间的预测实验，即使用一个季度的样本进行学习，然后对其相邻季度服装样本的评价进行预测。其操作步骤如下所述：选取春秋季的8套服装作为训练样本，根据样本数据特点调整神经网络参数，使网络进入稳定值域。对网络进行训练，得到训练后的最佳效果参数。

分别选取夏季与冬季各8套服装作为预测样本，进行评价值的预测。

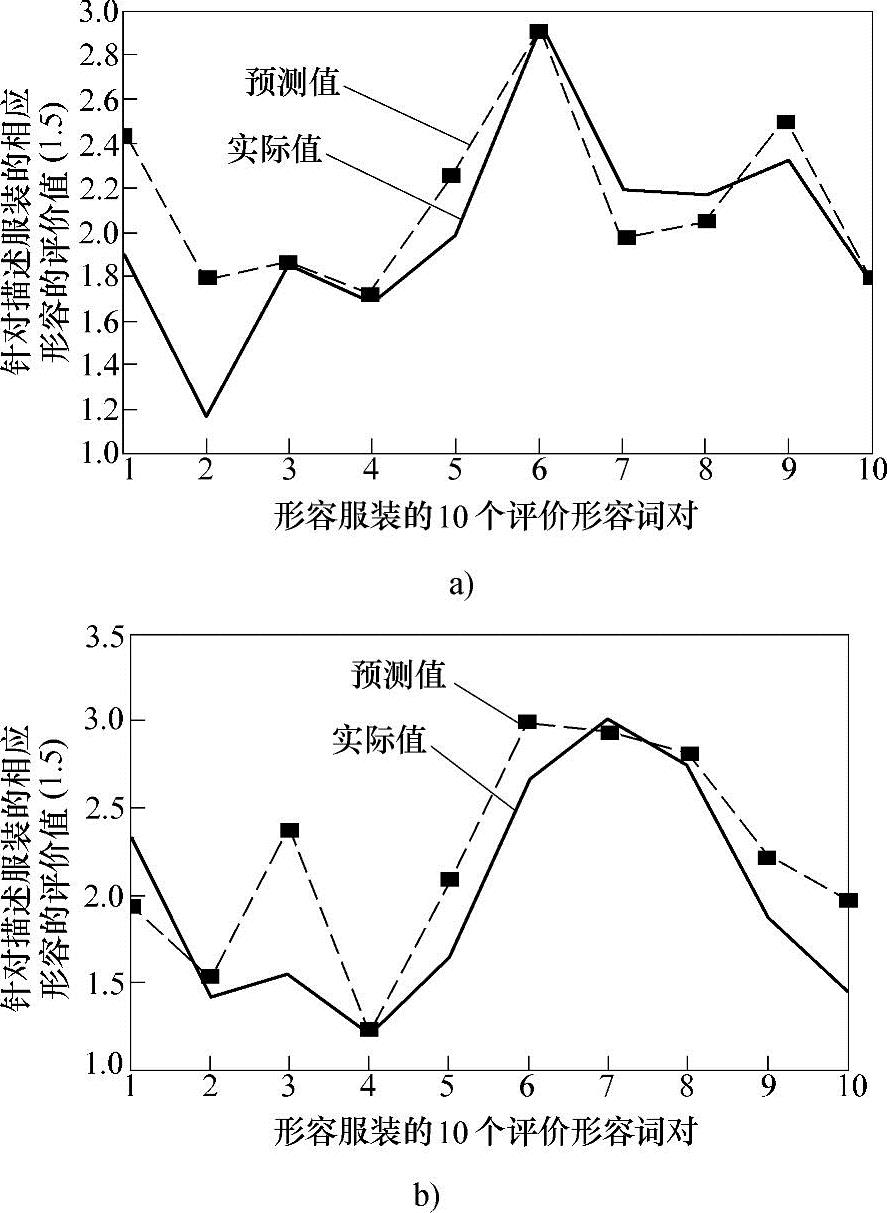
图6-27 相邻季节间预测实验效果

a）带有偏差单元的递归神经网络对服装评价的预测效果 b）带有偏差单元的递归神经网络对服装评价的预测效果

如图6-27所示，图a为以春秋季服装为训练样本，夏季服装为预测对象得到的预测效果，图b为同样以春秋季为训练样本，冬季为预测对象得到的预测效果。图中，实线为实际的评价值，虚线为网络输出的预测值。

再进行实验4——向反季节预测实验。基本步骤与实验3相同，不同的是训练样本服装选定为夏季，预测样本服装选定为冬季。图6-28为最终的预测效果。其中实线为实际的评价值，虚线为网络输出的预测值。

综合对比、分析实验2、3、4可以看出，从总体趋势来讲，预测效果是一个逐渐变差的过程。这也是可以理解的，因为不同季节的服装在样式上有较大的差距，它们之间的关联度也会相应地减弱，使用与关联度密切相关的人工神经网络方法进行预测时，这种现象的出现是必然的。由于预测服装的季节相关度不同，整体效果的变化过程可以从四个方面进行分析，见表6-8。

图6-28 带有偏差单元的递归神经网络对服装评价的预测效果

表6-8 季节相关度不同的预测实验效果比较

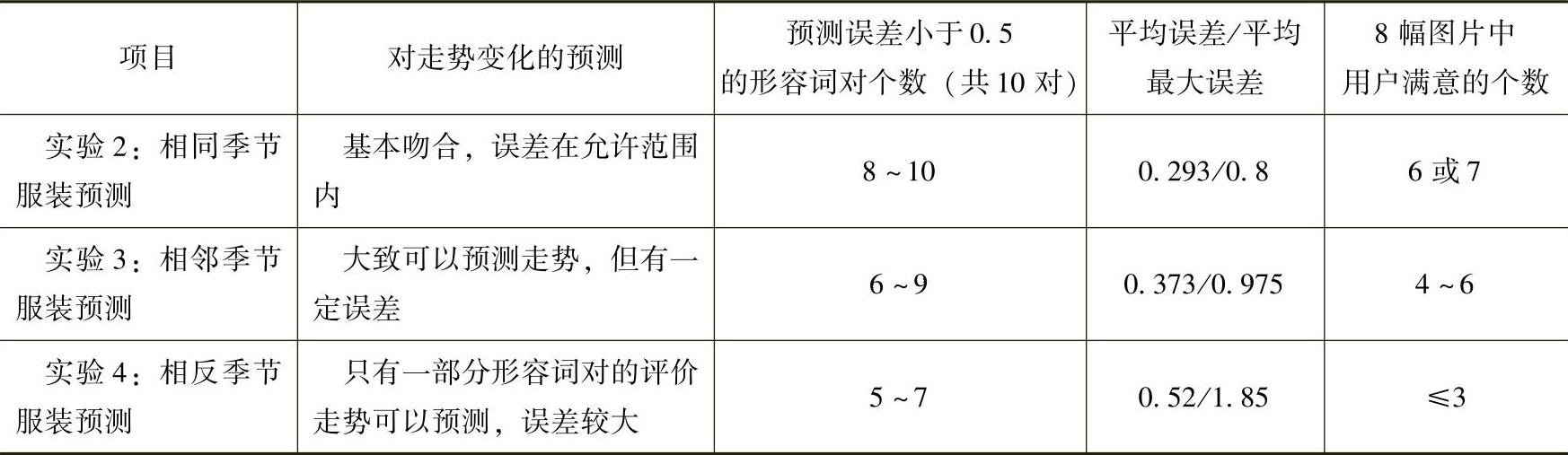
表6-8数据显示，即使在预测效果最差的实验4中，虽然在整体评价的走势上有较大出入，但仍然有近半数形容词对的预测误差小于0.5（之所以将误差的最大允许范围定为0.5，是因为用户在做出评价时的心理状态一般并不稳定，同时综合考虑到用鼠标拖动“滑块”时所带来的误差等原因），可以说使用这种带有偏差单元的递归神经网络，即使在训练样本数据与预测样本数据关联较小的情况下，仍能够在一定范围内模仿评价的效果。但是对比表格中2、4项可知，预测数据结果与用户实际的满意度还是有一定的差距，因此需要以更严格的用户实际满意度来决定一个方案的可行性。通过实验结果的对比，得到的结论是：使用带有偏差单元的递归神经网络只能进行相同和相邻季节服装的评价预测服务，相反季节服装的预测是不可行的。