人工心理的情感形式化方法在于把人类的情绪模型化和形式化,以便于在计算机人工系统中来模拟人类情感。
1.基于欧氏空间的人工情感数学模型
在科学研究中的一个常用研究途径就是,先把问题理想化和简单化,以试图寻求一些有意义的结论。为了去构造一个尽管与人类不尽相同但又合乎情理的情感表现,本模型针对计算机如何进行情感计算,提出一种情感空间的概率模型,并对其进行了计算机仿真。首先建立一个简单的情感空间模型,提出情感熵的概念,并根据情感熵来构造具有个性特点的且无外界影响的情感行为的概率转移矩阵,根据这样的概率矩阵来模拟一个无外界刺激的情感行为,即模拟一个封闭系统下的自由运动的情感模型。
(1)情感空间 在构造情感空间之前的一个首要问题就是,人的两种或两种以上具有矛盾的情感能否同时发生?关于这样的问题,心理学界仍在争论之中。而本模型则把这样的情感状态仍然考虑在所构造的情感空间中,但是其出现的概率将是足够小的。
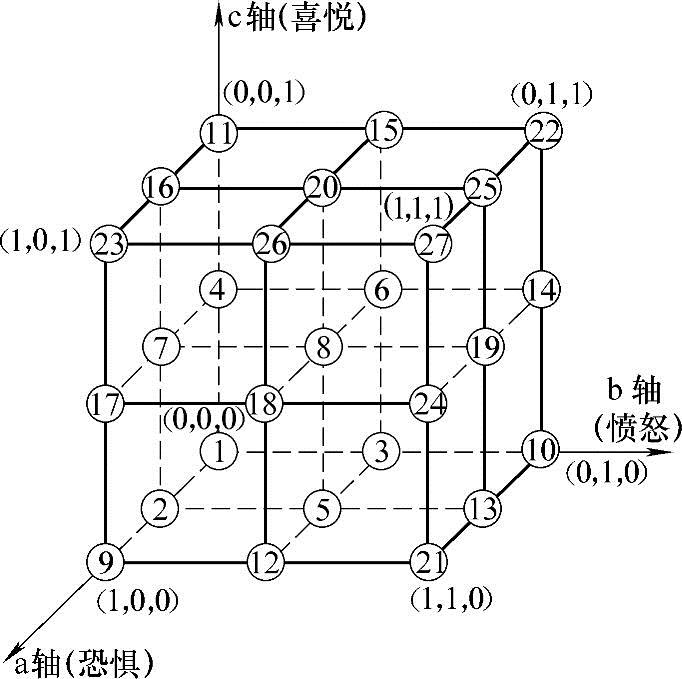
图3-27 三坐标情感的状态空间
这里从比较简单的三种情感:生气、害怕和高兴来构造一个情感空间,如图3-27所示。为进一步简化问题,我们规定,情感状态的每一个维仅取0、0.5、1三个数值。比如,就恐惧而言,则具有不恐惧(0)、有些恐惧(0.5)和恐惧(1)三个状态。于是在这样的三维情感空间里就具有27个情感状态。
那么很有意思的一点就是原点(0,0,0),这一点不仅仅代表为平静,而且还代表其他未知的情感状态。但在本模型中,仅考虑原点为平静状态的情况。
于是情感的活动就成为在这个情感空间的各状态的转移过程。自然这是一个马尔可夫的过程。如果更为一般的考虑,认为情感具有m种,其中每种情感可以划分为n个级别,于是这样构成的情感空间就具有nm个情感状态。令l=nm,于是得到l维的马尔可夫的概率矩阵如下:
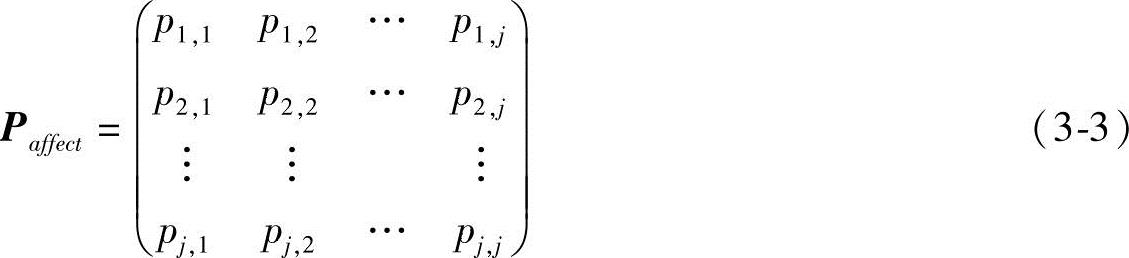
式中,pij为第i个情感状态到第j个情感状态的概率,并且满足如下关系:
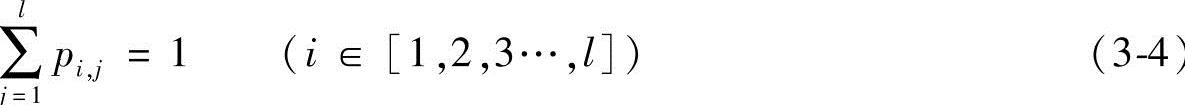
至此,就构建了情感变化的概率性模型。这样的情感空间把每个情感都细分为不同的强度,并且情感状态空间位置间的距离远近影响到转移的概率大小。
(2)情感熵 对于这样的情感空间及其概率的转移矩阵,该如何构造具体每个概率值,并能整体评判与度量所构造的情感的表现呢?熵,就成为了一个很好的数学工具。
对式(3-5)中表达的具有l个节点的m维情感空间,设某一时刻处于第i个状态,那么它到其他状态的概率就构成了一个情感变化的概率向量:
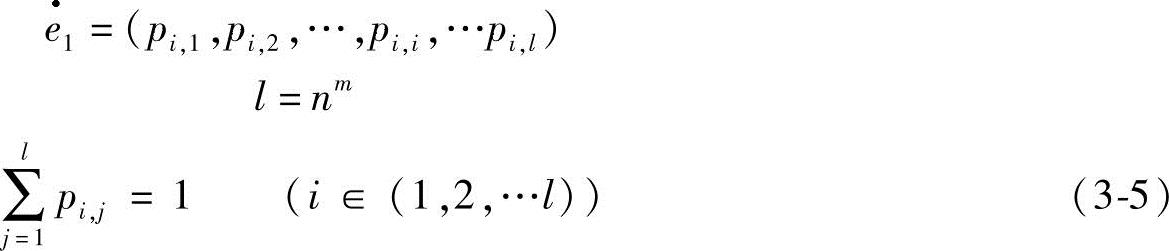
情感熵就定义为

式中,Ai为在第i种状态的情感熵;pij为第i种情感状态到第j种情感状态的概率;C为与对数底及单位选择有关的常数。
这里我们规定,在情感熵的计算过程中,对数的底是自然数,此时C值规定为1。在以后的讨论中,将遵循这样的约定。
情感熵表征了在某一时刻的情感变化的不确定程度,就是说当情感熵的值大时,意味着情感变化快,表现为一种性格的多变性;而情感熵的值小时,意味着情感变化缓慢。这也同时刻画了个体的特性。
通过建立情感空间,能够得到情感的各个状态的概率分布,从而可以计算出情感的熵值。利用情感熵可以对所得出的情感的概率分布进行评价。可以说,情感熵是描述情感的微观变化与宏观表现的桥梁。
(3)情感概率转移矩阵的构造 从对现实生活的观察,可以总结出以下几点概率分布方面的约束:
1)某一时刻情感空间里的某一情感状态,在下一时刻仍然处于本状态的概率是最大的。到其他情感状态的概率随距离的远离而单调下降。
2)在没有外界干扰的情况下,原点附近应是情感状态的平稳点。这就是说总的趋势是情感逐渐向原点(平静点)过渡。
3)具有相互矛盾的情感状态出现的概率最小。如既高兴又愤怒状态出现的概率是很小的。
另外,为了构造一个表现丰富的情感,各状态的转移概率在满足上述条件下,应该使其情感熵尽可能为最大。这类问题,就可以抽象为如下数学命题:
有一正数轴上的一个闭区间L:[1,m],某一事件落在此区间的概率为1,落在此区间上某一正整数i上的概率为pi,i∈(1,2,…,m),并有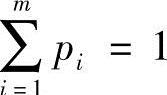 ,且
,且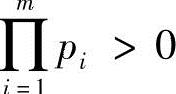 。现将此区间完全划分为n个非空子区间,n∈(1,2,…,m),记lk为第k个子区间,k∈(1,2,…,n),则有
。现将此区间完全划分为n个非空子区间,n∈(1,2,…,m),记lk为第k个子区间,k∈(1,2,…,n),则有 ,
,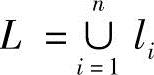 。令ai为第i个子区间内包含的整数的个数,ai∈(1,2,…,m)。记pi,j(i∈(1,2,…,n),j∈(1,2,…,ai))为事件落在子区间li上第j个非负整数点的概率。存在两个n-1项小于1的正数的数列ri、ki(0<ri<1,0<ki<1,i=1,2,…,n-1)。
。令ai为第i个子区间内包含的整数的个数,ai∈(1,2,…,m)。记pi,j(i∈(1,2,…,n),j∈(1,2,…,ai))为事件落在子区间li上第j个非负整数点的概率。存在两个n-1项小于1的正数的数列ri、ki(0<ri<1,0<ki<1,i=1,2,…,n-1)。
已知:m,n,ai,ri,并具有如下约束条件:
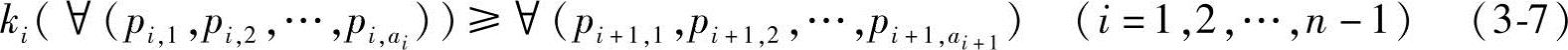
从式(3-7)中可以看出,约束条件已经包含在原点到其他节点距离之内了。
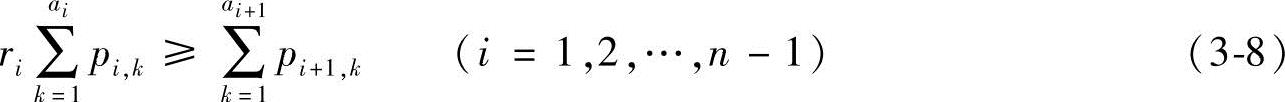
求:各满足如下最大值条件下的概率数列p1,p2,…,pn:

建立这个数学命题,目的在于对情感状态的变化进行数学描述、对情感的统计性规律进行表达。通过求解这样的命题,可以得到概率转移矩阵中的各个元素的具体数值,这样就构造出了具体的情感模型。
对于这样的命题,直接求解是困难的。用数值的方法并进行简化处理,可以寻找到其近似解。在得到情感空间的概率转移矩阵后,就可以模拟一个动态的情感变化的过程。首先需要设定一个初始的状态,即要设定在初始时刻,情感处于哪个节点上。那么要判定下一时刻情感将到达什么状态呢,这是具有概率性的行为。由于从一个节点到所有节点的概率和为1,那么就可以认为,每个节点的概率值就是一个区间的长度,所有的区间的长度的和就是1。
当按均匀概率分布产生一个0到1的随机数,这个数会落到某个区间内,于是就选中这个区间所代表的节点。在下一时刻,情感就转移到这个节点上。
(4)仿真及其分析 通过仿真试图找到一种方法,实现一个可理解的情感变化过程。也就是说,在没有外界干扰的情况下:情感状态是趋于平静的;然而情感是不可能绝对平静的,情感状态是有一定波动的;情感的未来状态是不确定的,但是又可以被“大概”猜测到的。因此对所构造出的情感模型去仿真模拟,来观察与上述的特点的相似程度。
下面根据不同参数的设定,进行模拟一个没有外界刺激的情况下的、情感的变化过程。为了具有典型意义,初始时刻的情感状态都选在离原点最远的节点。
设定维数为3、刻度数为5、敏感因子为0.6、初始状态处于第125个节点,一共进行200步的仿真,结果如图3-28所示。
设定维数为3、刻度数为5、敏感因子为0.3、初始状态处于第125个节点,一共进行200步的仿真,结果如图3-29所示。
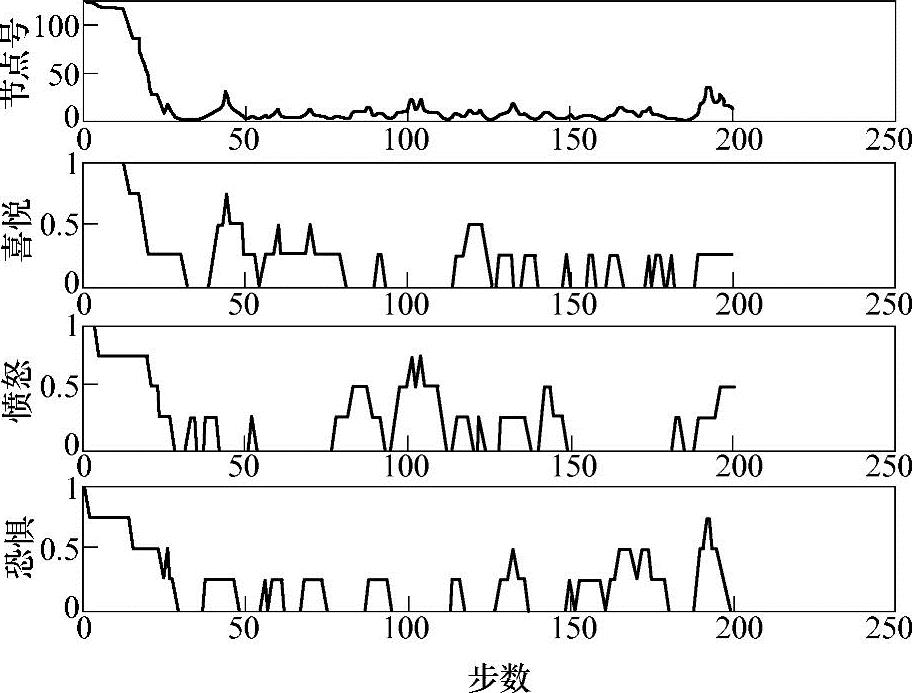
图3-28 情感回落与波动过程(维数为3、刻度数为5、敏感因子为0.6)
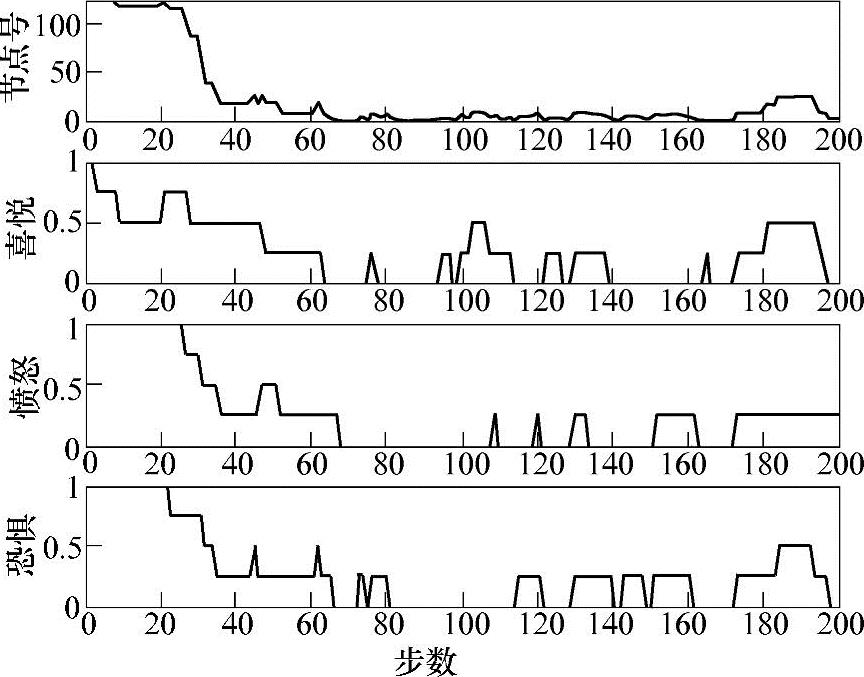
图3-29 情感回落与波动过程(维数为3、刻度数为5、敏感因子为0.3)
从仿真结果可以看出,在情感空间中,维数m是构造情感的基本出发点,是情感模型中所包含的基本情感的数量。在维数m确定的前提下,刻度数n代表了情感细腻程度。尽管刻度数n越大越好,但是会带来庞大维数的矩阵运算。敏感因子R的取值大小影响了情感的变化快慢。也就是,刻度数的提高或敏感因子的减小,都会降低情感的变化速度,同时降低了情感的动荡程度。
(5)结论 根据所构造的情感概率矩阵,建立了一个数学命题,其目的在于对情感状态的变化进行数学描述、对情感的统计性规律进行表达,并给出近似求解的数值算法。通过求解这样的命题,可以得到概率转移矩阵中的各个元素的具体数值,这样就构造出了具体的情感模型。通过用MATLAB仿真,可以直观地看到所模拟的情感变化过程。从中发现了在相同维数的情感空间下情感动荡的程度。在情感空间中维数确定的前提下,刻度数代表了情感细腻程度。敏感因子的取值大小,影响情感的变化快慢。刻度数的提高或敏感因子的减小,都会降低情感的变化速度,也就是降低了情感的动荡程度。
但是本模型没能对具有外界影响情况下的情感行为进行讨论、情感空间的概率描述中的约束规则还不是很完善等方面,都有待进一步研究。
2.基于马尔可夫链的情感计算建模方法
本模型的目的在于机器情感自动生成的基础理论研究。首先定义了情感的两种状态及其两个基本的变化转移过程,并应用马尔可夫链构造了一个情感概率空间,建立模拟情感变化的情感模型,给出了情感能量、情感强度和情感熵等概念,用以描述情感特征与情感状态。通过MATLAB的计算仿真,验证此模型可较好地模拟情感状态自发转移、变化的动态过程,可用于情感机器人的情感模拟计算,为情感计算和情感自动生成理论研究提供了一种新途径。
(1)情感状态的概率空间 根据基本情绪论,可把人类的情感状态分为几个基本类型。设情感状态空间集合S={si|i=1,2,…,N},N表示基本情感状态数。用随机变量X表示情感状态。设pi为X=si(取第i种情感状态)的概率,且满足
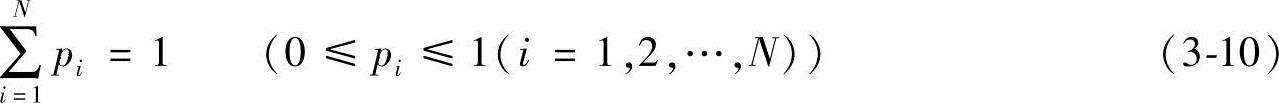
这样,情感状态的概率空间模型可表示成

设N=3,当X=s1、s2、s3时,分别表示高兴、愤怒、恐惧三种情感状态。在三维坐标空间中,用X轴表示p1,Y轴表示p2,Z轴表示p3,则情感状态可用三维坐标空间中的点(x,y,z)来表示,且满足下列方程:
x+y+z=1 (3-12)
0≤x≤1 0≤y≤1 0≤z≤1 (3-13)
由式(3-12)和式(3-13)可知,由式(3-10)所确定的情感状态点,始终在图3-30所示的正三角形ABC的范围内(包括边界),情感状态转移也限定在这个范围内,称为情感状态正三角形概率空间。该正三角形的中心可作为情感的平静状态,此时p1=p2=p3=1/3。当N=4时,情感状态点位于一个正四面体内部和边界上。概括地说,情感状态点为由式(3-12)所确定的超平面上的一个凸集,称为情感状态超正三角形概率空间。情感状态的划分如图3-31所示。
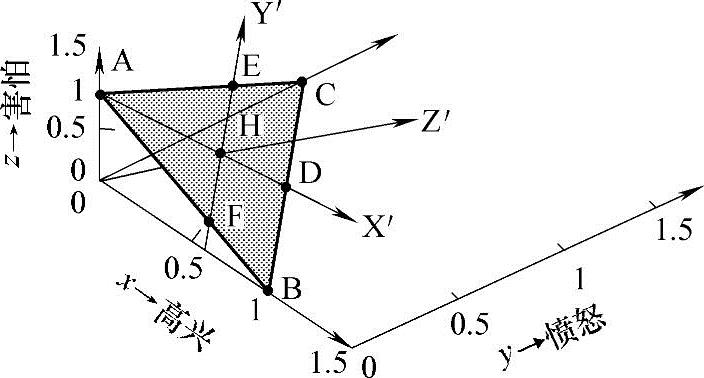
图3-30 情感状态正三角形概率空间
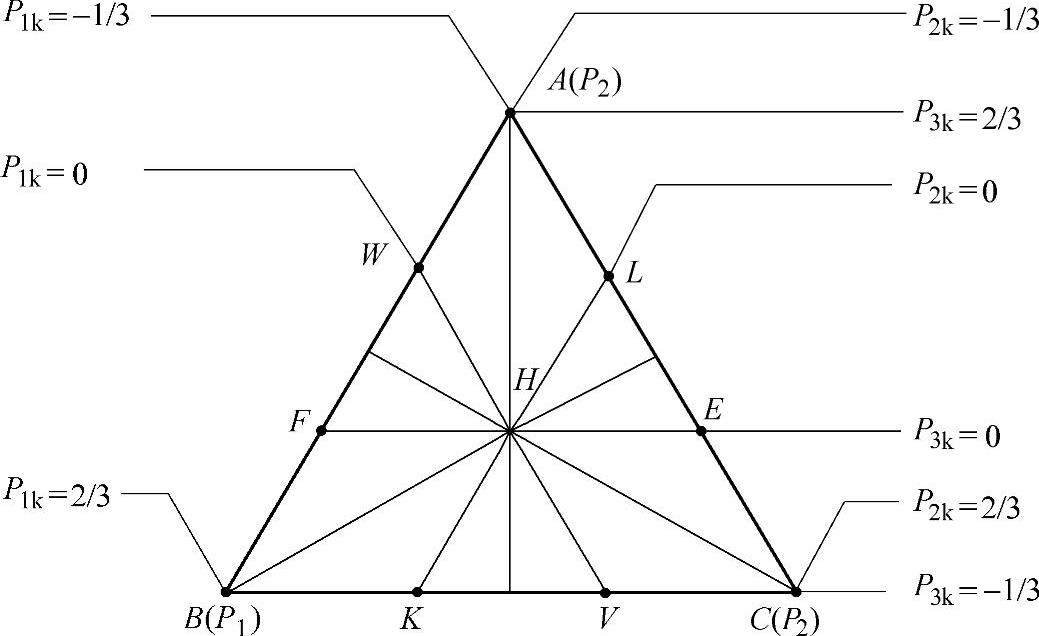
图3-31 情感状态划分示意图
(2)情感状态的变化过程 在没有刺激的情况下,情感状态主要表现为心情状态。这时发生的过程是心情状态自发转移。此时用P(n)=[p1(n)p2(n)p3(n)]表示在时刻n的心情状态的概率分布,称为当前心情状态概率分布,用P(0)=[p1(0)p2(0)p3(0)]表示在时刻0的心情状态的概率分布,称为初始心情状态概率分布。心情状态自发转移可用马尔可夫链的转移过程来描述。
当情感机器在第n时刻受到外部刺激时,将发生在刺激的作用下的情绪状态刺激转移过程,此时的P(n)将作为情绪状态刺激转移过程的出发点,称为情绪状态转移的初始概率分布,用π=[π1π2π3]表示,则πi=pi(n)(i=1,2,3)。
情感状态从π开始,在强度为T的刺激的作用下,按基于隐马尔可夫模型(HMM)而建立的情绪状态刺激转移模型进行转移,最后达到情绪状态P(T)。此时,应将根据情绪状态的类型和强度,产生相应的表情和情感行为。之后情绪状态P(T)将转化为初始心情状态概率分布,即P(0)=P(T)。
HMM可用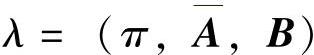 来表示。其中,
来表示。其中,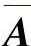 为情绪状态刺激转移矩阵,可表示机器的情感性格;B为观察值矩阵,可表示刺激的情况。
为情绪状态刺激转移矩阵,可表示机器的情感性格;B为观察值矩阵,可表示刺激的情况。
我们把由下面的公式:

所定义的H(X),称为情感熵。情感熵越大,系统各种情感状态在总体上的不确定性就越大,表现某种情感状态的倾向性也越小;反之,情感熵越小,系统各种情感状态总体上的不确定性就越小,表现某种情感状态的倾向性也越大。如果pi分别用pi(n)、pi(T)和矩阵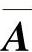 的极限概率
的极限概率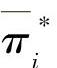 来替换的话,那么H(X)则分别表示心情熵、情绪熵和情感性格熵。
来替换的话,那么H(X)则分别表示心情熵、情绪熵和情感性格熵。
(3)基于马尔可夫链的心情状态自发转移 马尔可夫链的基本方程可表示为
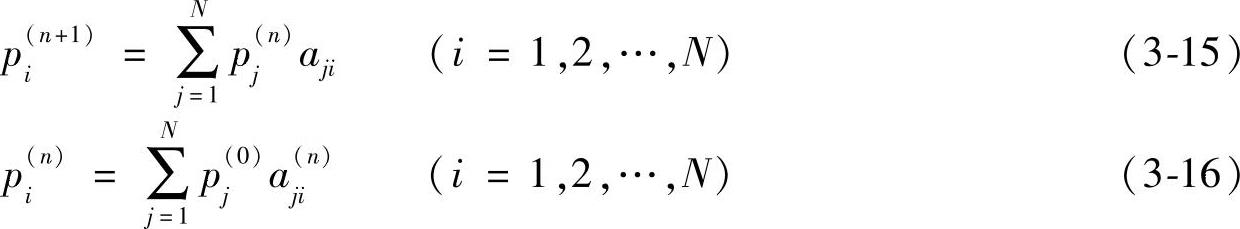
其矩阵形式可表示为

式中,P(n)和P(0)为前述的当前心情状态概率分布和初始心情状态概率分布;A为心情状态自发转移矩阵。
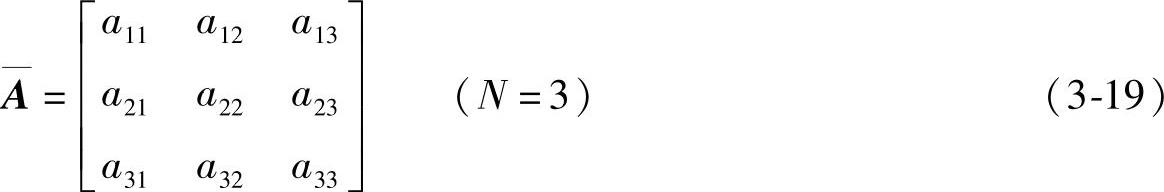
心情状态自发转移过程相对比较缓慢,可通过心情状态转移矩阵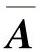 的参数来控制,同时心情状态的自发转移应该从P(0)开始向平衡点缓慢转移,所以
的参数来控制,同时心情状态的自发转移应该从P(0)开始向平衡点缓慢转移,所以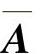 的极限概率分布可以表示为
的极限概率分布可以表示为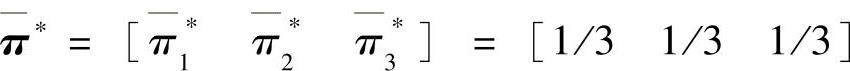 。
。
给定极限概率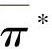 怎样确定矩阵A中的各个分量aij(i,j=1,2,3)呢?在心情状态自发转移和情绪状态刺激转移过程中,都需要解决这一问题。然而,当给定
怎样确定矩阵A中的各个分量aij(i,j=1,2,3)呢?在心情状态自发转移和情绪状态刺激转移过程中,都需要解决这一问题。然而,当给定 时,对应转移矩阵
时,对应转移矩阵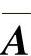 中的各个分量aij(i,j=1,2,3)并不是惟一的,而是有无穷多个,不同的组合,将对转移过程产生影响。那么怎样确定这些分量呢?下面给出一种方法。
中的各个分量aij(i,j=1,2,3)并不是惟一的,而是有无穷多个,不同的组合,将对转移过程产生影响。那么怎样确定这些分量呢?下面给出一种方法。
令
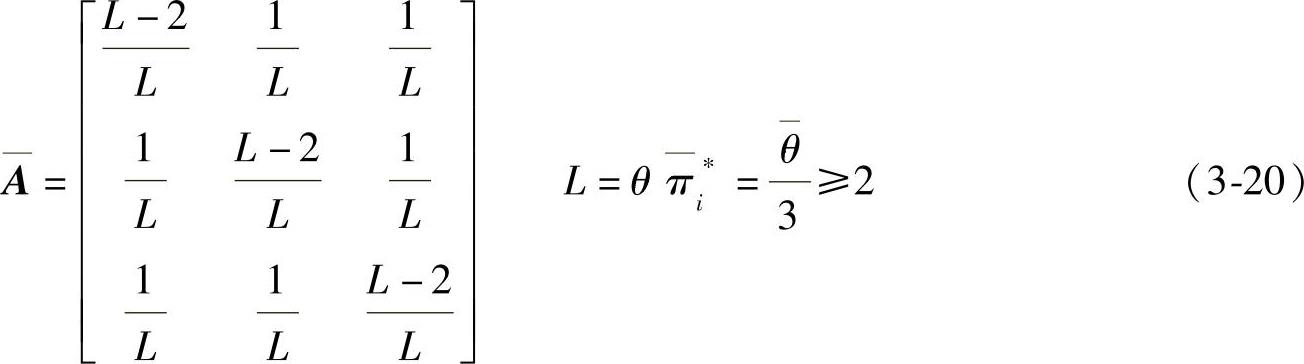
其特征方程
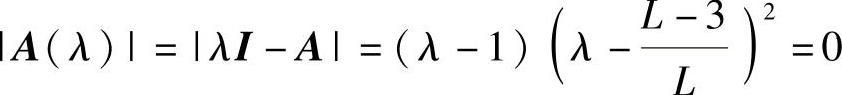
的根,即特征根为

在λ=1为单根的情况下,可利用下面的公式:
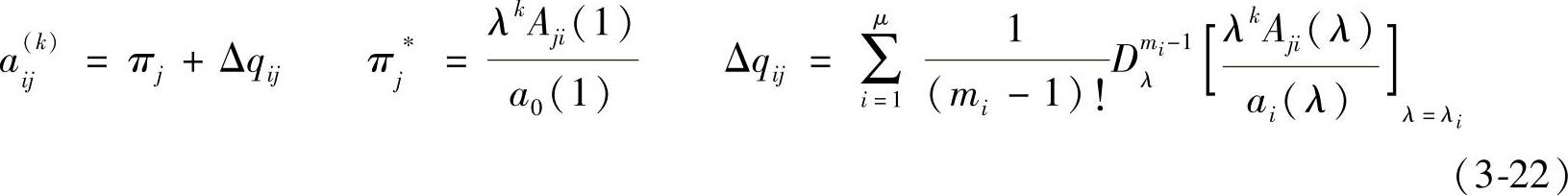
来计算矩阵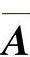 中的元素,得到结果为
中的元素,得到结果为
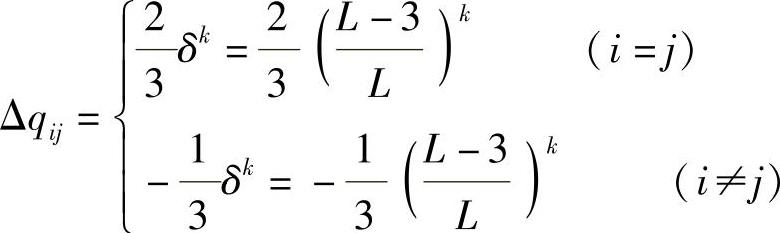

根据式(3-15)经计算得
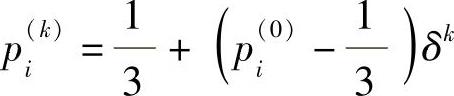
即

式中
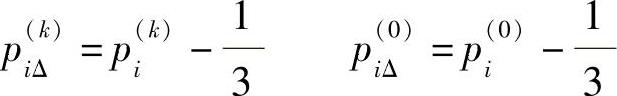
其中,piΔ(k)、piΔ(0)表示对第i种情感状态的当前和初始情感强度,按指数规律变化,参数L或θ可调整心情状态自发转移速率。其仿真曲线如图3-32所示。
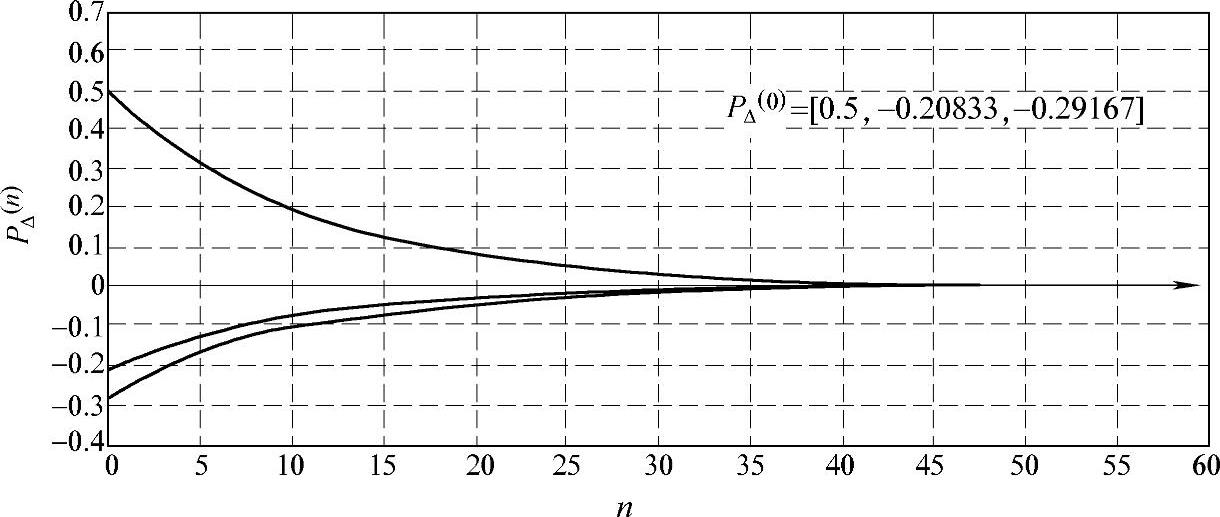
图3-32 θ=100,心情状态自发转移过程PΔ(n)-n曲线
(4)情感能量 按照奥地利著名精神病学家、心理学领域的新学派——精神分析学的创始人弗洛伊德的观点,人类所有的心理活动,不论是思想还是行动,都需要能量。弗洛伊德认为,有三种能量概念特别适合于解释人类行为:能量守恒、熵、运动和潜在能量之间的差别。据此也可以认为情感过程需要能量,把情感机器产生各种情感的能力称为情感能量,用E表示,情感状态的变化过程实际上可看成是情感能量重新分配的过程。设N=3,则分配给三种不同情感状态的能量分别用E1、E2、E3表示,其能量比例为
ei=Ei/E,(i=1,2,3) (3-25)
平均能量为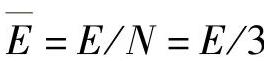 ,则情感强度可表示为
,则情感强度可表示为
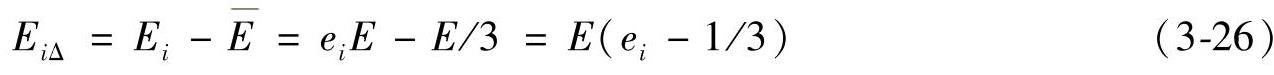
如果E为常数,且设为1的话,则EiΔ=ei-1/3=pi-1/3=piΔ。式(3-10)中的概率分布实际上也是情感能量的分配比例。
(5)情感状态的分区 可根据情感强度将图3-30中的情感状态的概率空间进行划分。piΔ=0,表示情感状态i处于中性,以此为基准,当piΔ>0时,则情感状态i处于激发状态,也就是说,情感机器应该表现出该情感状态;当piΔ<0时,则情感状态i处于抑制状态,也就是说,情感机器不仅不表现出该情感状态,而且还需要很大的外界刺激才能达到一定的正向强度。其划分情况见表3-4。
表3-4 根据情感强度对情感状态空间的分区

(6)结论 根据上面的讨论,可得到下述结论:
1)由式(3-10)知,在任意时刻,各情感状态的概率之和为1,或者说在任意时刻,分配给各情感状态的能量之和等于总能量;
2)由结论1)可得出,在任意时刻,各情感状态的情感强度之和总为零。这说明各情感状态是互相排斥的,一种状态的强度增加,必然会使其他情感状态的强度减少;
3)情感能量的变化应该是连续的,而不能突变。可以假定k时刻的能量分配eki(I=1,2,3)只与前一时刻的能量分配ek-1i(i=1,2,3)相关,而与以前时刻的能量分配ek-2i、ek-2i、Λ、e0i(i=1,2,3)无关。也可以说,k时刻的情感状态的概率分布pki(i=1,2,3)只与前一时刻的概率分布pk-1i(i=1,2,3)相关,而与以前时刻的概率分布pk-2i、pk-2i、Λ、p0i(i=1,2,3)无关。这正是马尔可夫过程的无后效性,据此可以用马尔可夫链来描述情感的转移过程。
4)在没有外界刺激的情况下,可以用一个马尔可夫链来描述心情状态的自发转移过程,并假定总是向平静点H转移;在有外界刺激的情况下,可以采用一个两重马尔可夫链,即HMM来描述情绪状态的刺激转移过程,这里不做深入讨论。
综上所述,本模型所提出的情感计算的基本概念和建模方法,经理论推导和仿真计算、验证,其符合人类情感变化规律,为情感自动生成理论的深入研究奠定了基础,也为建立更为理想的情感计算模型提供了一个新的途径。
3.基于自组织理论的人工心理建模
该模型在人工心理理论的基础上,根据心理学上普遍使用的基本情绪理论构建了一套模型。该模型分为两部分:一部分以外界刺激为输入,描述了人的情绪在受到外界刺激的情况下的转变,以及如何做出反应;另一部分则描述了人的心理在无外界刺激的情况下,如何向平静状态转变的过程。该模型中认为人的情绪转变是一个复杂的过程,单一的数学理论是无法准确地描述的,因此采用了自组织理论、模糊数学、最优化理论中的模拟退火算法等多种数学理论方法,以期望能近似准确地描述人的整个心理过程。
(1)模型构建 模型分两部分构建:接受外界刺激部分和无外界刺激部分。模型总体设计框图如图3-33所示。
1)接受外界刺激的模型:根据心理学理论,考虑基本情绪、内驱力、外界刺激三者及三者之间的联系。
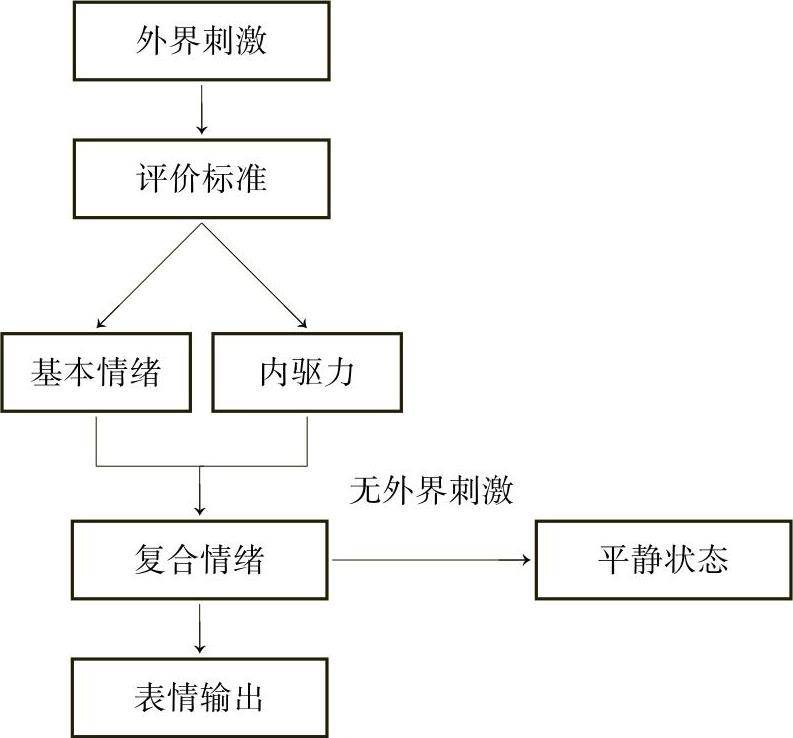
图3-33 基于自组织理论的人工心理模型总体设计框图
首先考虑基本情绪,这里借用自组织理论的一些思想。德国哲学家康德认为,自组织的自然事物具有这样一些特征:它的各个部分即使有其他部分的作用而存在,又是为了其他部分、为了整体而存在的;各部分交互作用,彼此产生,并由它们之间的因果连接而产生整体。该模型认为人的心理过程也是一个自组织的过程,德国科学家H·哈肯创立的协同学理论在自组织方法论中处于一种动力学方法论的地位,它是体系自身如何保持自组织活力的重要方法。先考虑单独的一种基本情绪,比如说快乐。情绪的强度是情绪最明显的性质,起着序参量的作用,记情绪的强度为P(t),P(t)是按外界刺激强度变化的,而外界刺激的强度A的确定又与当时情绪的强度有一定的正比例关系,引入AP(t)项,再考虑到情绪随时间的推移会趋于平静,引入-BP2(t)项,用这种考虑所得到的方程为

式中,A≥0,B>0;初值为P0。方程的解为
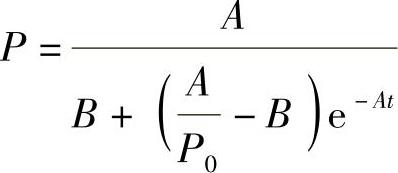
当t→∞时,P(t)→A/B,即情绪最终趋于稳定值A/B。A为外界刺激参数;B为事先给定值,用来反映人的情绪类型。B值大时,A/B值小,可认为此人情绪不易激动;反之,B值小时,A/B值大,可认为此人情绪易激动。
由八种基本情绪可确定八个这样的方程:
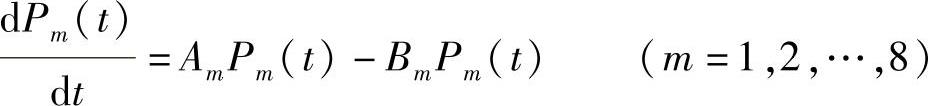
现在,来确定Am的取值。由于人类的意识形式的多样性,即使是对同样的一个外界刺激,不同人的感受也会有所不同。现在,还没有一种通用的方法能准确地描述不同人对外界刺激的感受程度。因此,由计算机来确定刺激量Am是不够准确的,甚至有时会与实际有很大差别。所以这里采用了由人来评判事件对人的刺激量Am的方法,以期望得到与实际相符合的刺激量Am。Am的取值通过评价的方法来得到。根据普拉切克的八种情绪的五点记分量表来设计评价体系。评价的指标集为
①U={快乐,接受,惊奇,惧怕,悲伤,厌恶,兴趣,愤怒}
②评价分为五个等级γ={无,微,中,强,极强},对应的数值为{1,2,3,4,5}
对于一个外界刺激事件,随机抽取100个人,让他们对此事件根据以上指标集做出等级选择。结果比如说,对于快乐这一指标,10%的人选择等级“无”,10%的人选择“微”,20%的人选择“中”,30%的人选择“强”,30%的人选择“极强”。A1的值最终确定为γ1的数学期望E(γ1)=0.1×1+0.1×2+0.2×3+0.3×4+0.3×5=3.6。
这样可得到A的向量
(A1,A2,A3,A4,A5,A6,A7,A8)
这样得到的A值与实际是相符的。
得到A后,便可依据基本情绪方程计算出基本情绪为
P(P1,P2,P3,P4,P5,P6,P7,P8)
数学上描述可认为内驱力也是一个8维的向量δ(δ1,δ2,δ3,δ4,δ5,δ6,δ7,δ8)。
在此模型中,内驱力实际上是用来表征人的行为意志的量。用此量来调控情绪,此量与人的处事态度有关,对于做同样一件事情,个人的内驱力是不同的。正是由于内驱力与事件的相关性,所以内驱力的取定,需要由外界刺激来决定。可认为,外界刺激在哪一个分量上比重大,内驱力在该分量上的值也就会相应要大一些,但并不是成正比的关系,其中还夹杂着个人的主观意识。现在借用模糊数学中隶属函数的概念,给出一种确定内驱力数值的方法:
将外界刺激强度A的分量做归一化处理,记
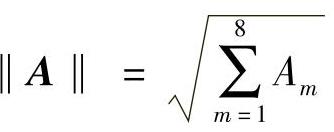
令
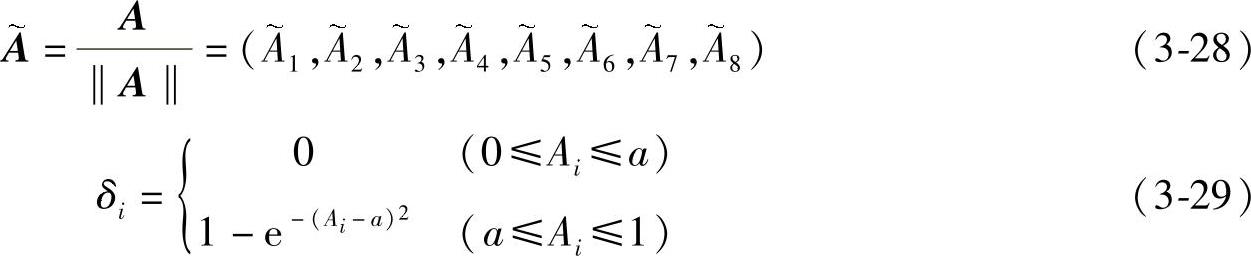
以上只是给出了一种隶属函数,实际上隶属函数可根据人的态度曲线来确定。比如说,给定一条态度曲线,便可采用BP神经网络来实现。以此曲线作为教师信号,反复训练神经网络,便可得到与曲线近似吻合的隶属函数。
现在考虑一下内驱力与复合情绪之间的关系。由于一个人在情绪高涨时,做事的动力也会增加,所以可认为情绪对内驱力是起加强作用的。同样,人在做事欲望强时,情绪也更容易波动,所以可认为内驱力对情绪也是起加强作用的。可认为情绪与内驱力都有自发衰退的趋势。根据以上理论,可用数学表达式描述两者关系如下:

式中,s为复合情绪中某一种情绪强度;u为与内驱力对应的该种情绪的分量强度;α为内驱力的衰减系数,α>0;β为情绪的衰减系数,β>0。下面用精确消去的方法求解此方程组。
直接求解式(3-31)得

进行分部积分,得
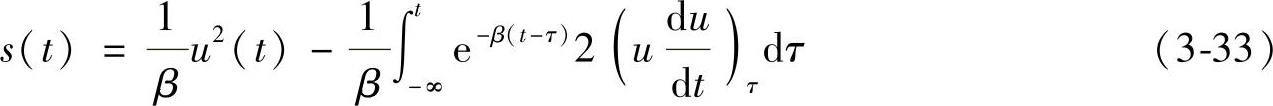
将式(3-30)代入式(3-33)得
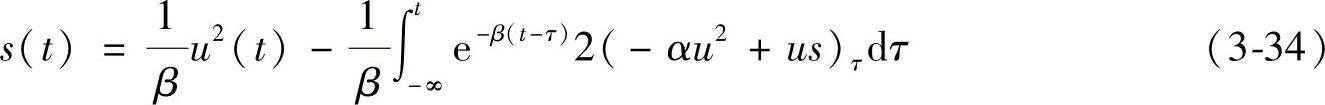
再进行迭代,有
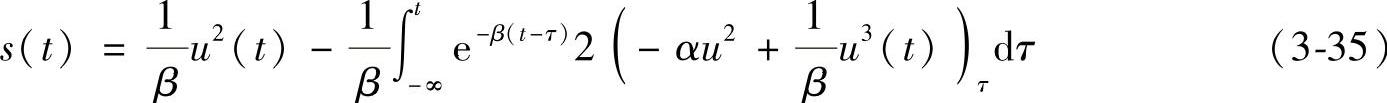
这样反复进行分部积分和迭代,得
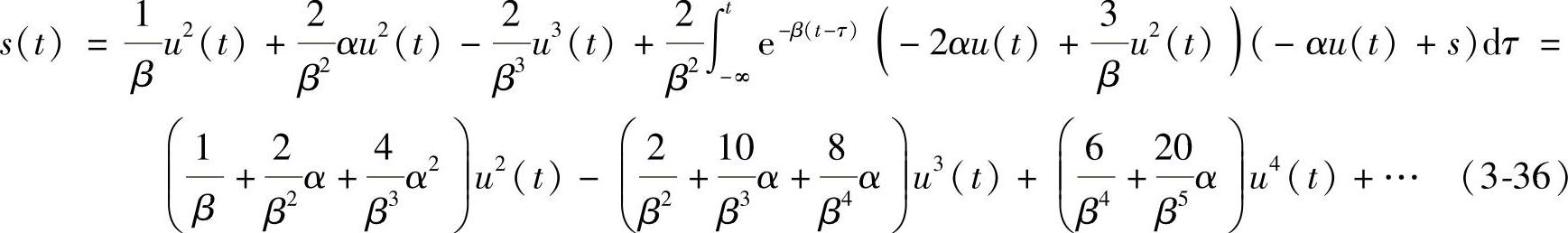
多次利用迭代和分部积分后,s(t)即可用u(t)的幂级数表示出来。若u(t)足够小,则s(t)就可以用前面的少数几项来表示。由外界刺激决定内驱力的表达式可看出0≤u<1,且一般情况下得到的u都比较小,所以可认为满足条件,忽略高阶次项,取s(t)的近似表达式得
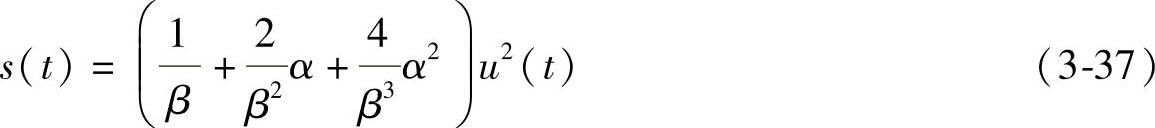
因此,在考虑复合情绪的数学描述时,又考虑到基本情绪对复合情绪的影响,可认为复合情绪由下式决定:(www.daowen.com)
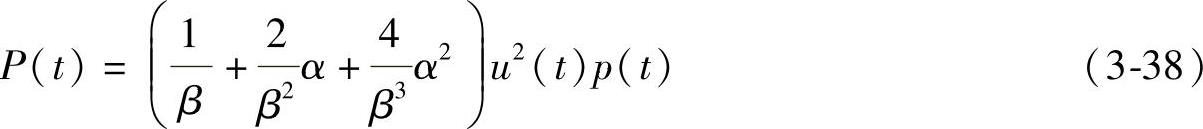
式中,P(t)为复合情绪;u(t)为内驱力;p(t)为基本情绪;α、β为常数,与人的个性、敏感度有关,起着调控人情绪波动幅度的作用。
复合情绪的向量形式为
(δ1p1,δ2p2,δ3p3,δ4p4,δ5p5,δ6p6,δ7p7,δ8p8)
式中,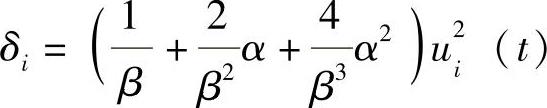
2)无外界刺激的模型:在无外界刺激的情况下,刺激输入的情感模型不再适用,在这种情况下,可认为情绪自发地向平静状态转变。在这种情况下,可以认为基本情绪在内驱力作用下自发向平静状态转移。该模型给出一种内驱力与基本情绪之间关系的描述方法。一般说来,人对事情的态度与情绪正相关,情绪越高,做事越积极。而做一件事的动力也会因做事时间的延长而逐渐消退,所以可认为内驱力既自发衰减又在基本情绪作用下正向加强。基本情绪则在内驱力的影响下逐渐衰减,衰减速度与自身相关。自身强度越大,衰减越快。这与实际也是较相符的。现给出由以上理论构建出的数学的描述式:
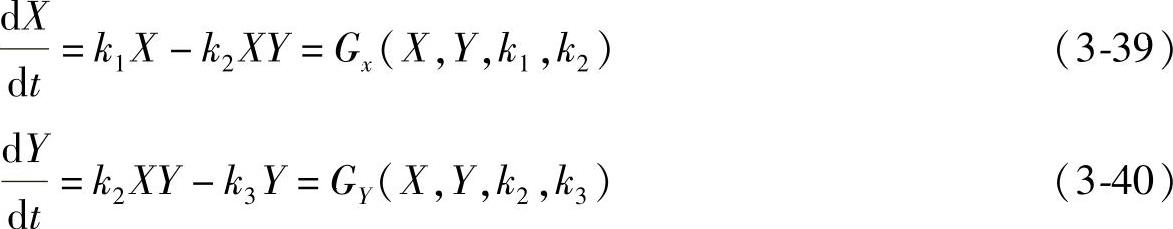
式中,X为一种基本情绪强度;dX/dt为情绪强度变化律;Y为内驱力对应该基本情绪的分量的强度;dY/dt为内驱力变化律;k1为基本情绪的增加系数;k2为基本情绪的衰减系数,同时也是内驱力的增加系数;k3是内驱力的衰减系数。
现先求解此方程组,由定态条件dX/dt=dY/dt=0,可得
k1X=k2XYk2XY=k3Y (3-41)
虽然X=Y=0也满足上式,但无意义,故有意义的定态解是

由于情绪总会受到微小的扰动,所以对定态解进行稳定性分析。首先写出并求解定态解附近扰动的演化方程,然后分析扰动的渐近行为,令
X=X0+xY=Y0+y (3-43)
且有
|x|<<X0 |y|<<Y0
将式(3-43)代入式(3-42)
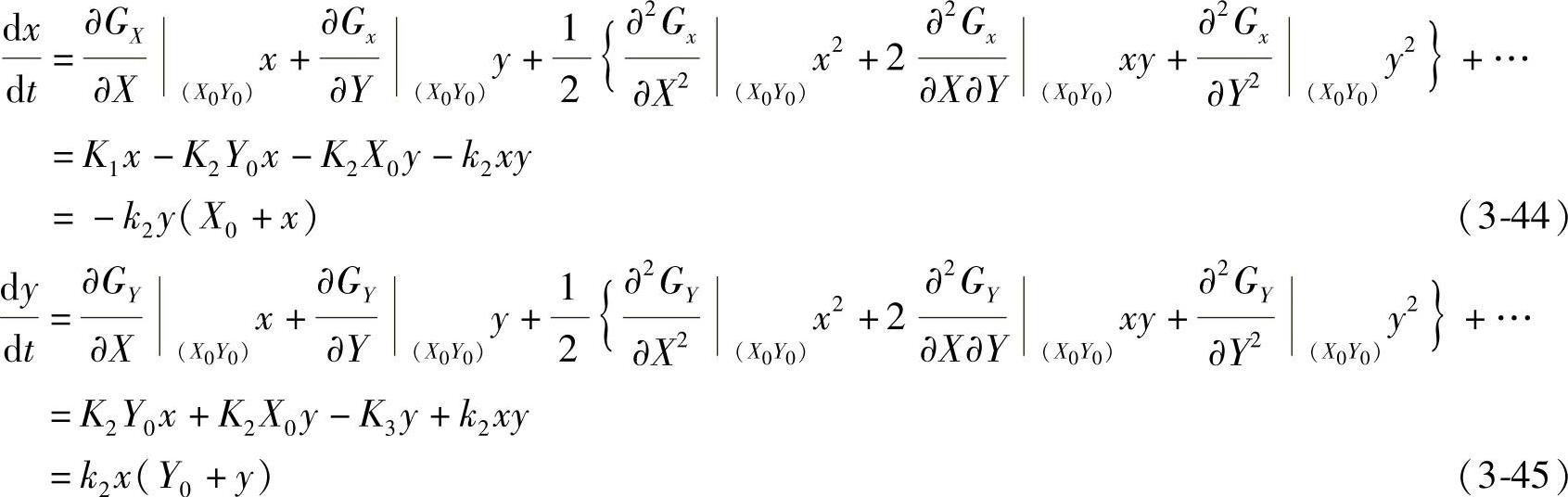
式(3-44)和式(3-45)是扰动x、y服从的演化方程。忽略高阶次量xy,可将它们线性化,而得到扰动服从的线性方程组:
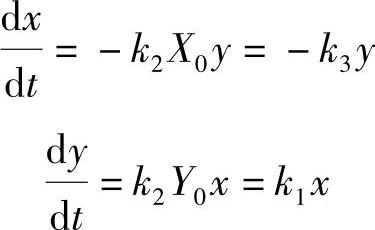
写成矩阵形式为
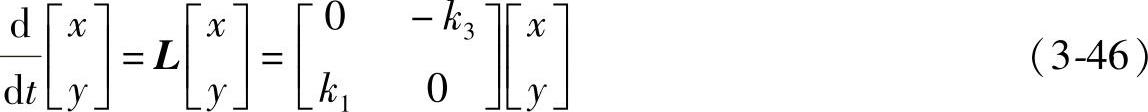
线性方程式(3-46)的解为

λ由下列特征方程决定:

式(3-48)有非零解的条件是
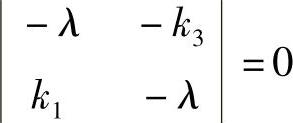
或λ2+k1k3=0,即

即λ为纯虚数,式中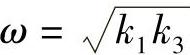 。将式(3-49)代入式(3-47),则有
。将式(3-49)代入式(3-47),则有

式(3-50)说明,设t=0时,情绪处于偏离定态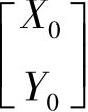 的某一初态
的某一初态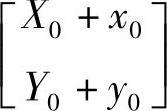 ,则随着时间的增长,情绪既不会无限地远离,也不会无限地趋于定态,而是简单地围绕定态
,则随着时间的增长,情绪既不会无限地远离,也不会无限地趋于定态,而是简单地围绕定态 振荡。振荡的圆频率是
振荡。振荡的圆频率是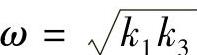 。这一结果描述了情绪稳定后围绕平静状态上下波动的情况,与实际是相符的。
。这一结果描述了情绪稳定后围绕平静状态上下波动的情况,与实际是相符的。
考虑到情绪的连续性,情绪恢复到平静的过程不可能是一个大的阶越过程,而应该是一个缓慢发展的过程。这里引用协同学中的最大信息熵原理来描述这一过程。最大信息熵原理认为,在非平衡相变点处,系统将要演化到的有序状态(分布函数的)信息熵在各种可能状态中具有最大值。借用这一思想,该模型引进人工心理理论中的情感熵的概念,即情感熵是描述情感的微观变化与宏观表现的桥梁。其数学形式为
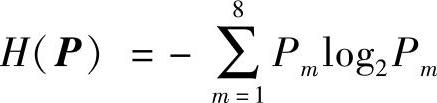
对复合情绪的分量做归一化处理,记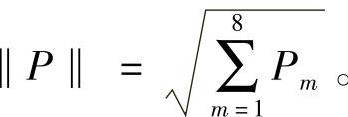 令
令
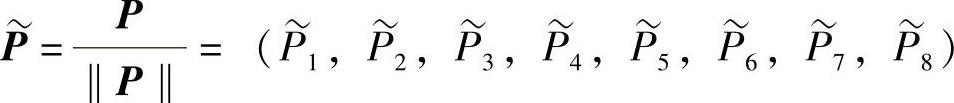
可认为复合情绪处在各基本情绪的概率为其对应分量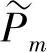 ,给出一种心情平静状态的定义:当复合情绪处在各基本情绪概率相等时,为心情的平静状态。也就是在情感熵最大时,心情处在平静状态。认为情感熵越大,心情越趋于平静状态。
,给出一种心情平静状态的定义:当复合情绪处在各基本情绪概率相等时,为心情的平静状态。也就是在情感熵最大时,心情处在平静状态。认为情感熵越大,心情越趋于平静状态。
现在给出一种模拟心情趋于平静过程的方法。采用最优化理论中的模拟退火算法来模拟心情自发趋于平静的过程。它与心情平静过程都是自发过程,具有一定的相似性。
模拟退火算法是基于金属退火的机理而建立起来的一种全局最优化方法,它能够以随机搜索技术从概率的意义上找出目标函数的全局最小点。模拟退火过程的构成要素如下:
①搜索空间Ω:搜索空间也称为状态空间,它由可行解的集合组成,其中的一个状态x就代表一个可行解。在情感空间中,一个复合情绪状态就代表一个可行解。
②能量函数E(P):能量函数也就是需要进行优化计算的目标函数,其最小点为所求的最优解。取情感熵的负值为能量函数,即
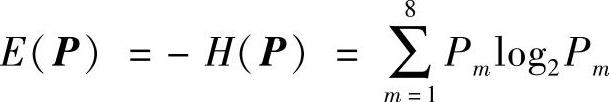
③状态转移规则p:状态转移规则是指从一个状态Pold向另一个状态Pnew的转移概率,它与当前的温度参数T有关。
④冷却进度表T(t):冷却进度表是指从某一高温状态T0向低温状态冷却时的降温管理表。
假设时刻t的温度用T(t)来表示,经典模拟退火算法的降温方式为
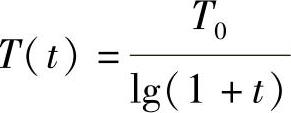
而快速模拟退火算法的降温方式为
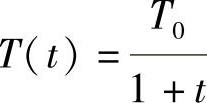
这两种方式都能够使得模拟退火算法收敛于全局最小点。
假设在状态Pold时,系统受到某种扰动而可能会使其状态变为Pnew。与此相对应,系统的能量也可能会从E(Pold)变成E(Pnew)。系统由状态Pold变为状态Pnew的接受概率可由下面的Meteopolis规则来确定:
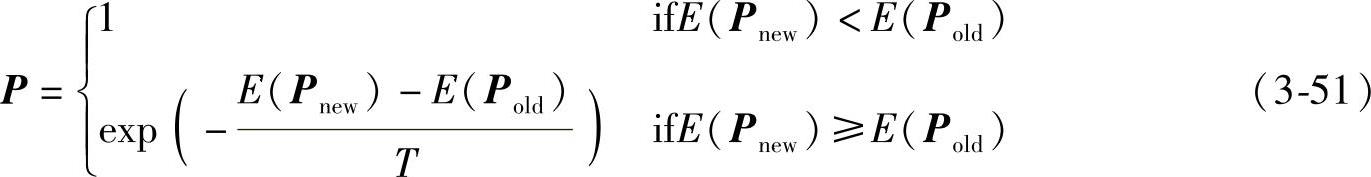
上式的含义是:当新状态使系统的能量函数值减少时,系统也一定接受这个新的状态;而当新状态使系统的能量函数值增加时,系统也以某一概率接受这个新状态。
固定温度参数T,反复进行状态转移过程,接受概率p(x)将服从Gibbs分布:

式中,Z是使概率值正规化的系数。
由上式可见,随着温度参数T的减小,接受概率也逐渐减小,最后系统会收敛于某一能量最小的状态,该状态就可作为目标函数的全局最小值。对应于情感模型也就是心情的平静状态。
其具体算法如下:
①以当前心情状态点为初始最优点,计算目标函数值(即能量函数值)。
②设置初始温度θ←T0。
③设置时间参数t←1。
④对当前最优点作一随机变动,产生一个新的最优点,计算新的目标函数值,并计算目标函数值的增量Δ。
⑤如果Δ<0,则接受该新产生的最优点为当前最优点。
⑥如果Δ≥0,则以概率p=exp(-Δ/θ)接受该新产生的最优点为当前最优点。
⑦如果t<终止时间,则t←t+1,转向第④步。
⑧如果未达到冷却状态,则:θ←T(t),转向第③步。
⑨如果已达到冷却状态,则输出当前最优点,计算结束。
3)输出反应:参照图3-5所示的面部表情与情绪对照规则,这里给出一种基于表情的机器情绪对应关系。
①在接受刺激的模型中,复合情绪的数值范围是可以确定的,根据其数值范围,将每一种情绪分为五个等级:无、微、中、强、极强,对应每一种情绪的每一种强度给出一种或几种表情。
在最终的复合情绪确定以后,依次从大到小取其分量,使得分量之和大于给定的阈值(比如60%),再根据这些分量的情绪的强度,取出对应的表情输出。设取出的分量为喜悦,对应其情绪强度为中,则输出表情如图3-34所示。

图3-34 输出表情
②在无外界刺激的模型中,采用类似方法,从输出的情绪中,依次从大到小取出比例最大的分量,直到超过阈值,用此分量值乘以‖P‖,得到情感强度,再从表情表中取出其表情,并输出。
(2)仿真及分析 仿真的目的在于给出此模型的实现,并分析情感的变化过程和转移规律。在有外界刺激时,根据接受外界刺激的模型,动态地模拟人的情感变化过程和表情变化过程。在情绪稳定以后,再模拟人情绪向平静状态转化的过程,绘出转移曲线。图3-35所示为接受刺激模型仿真界面。
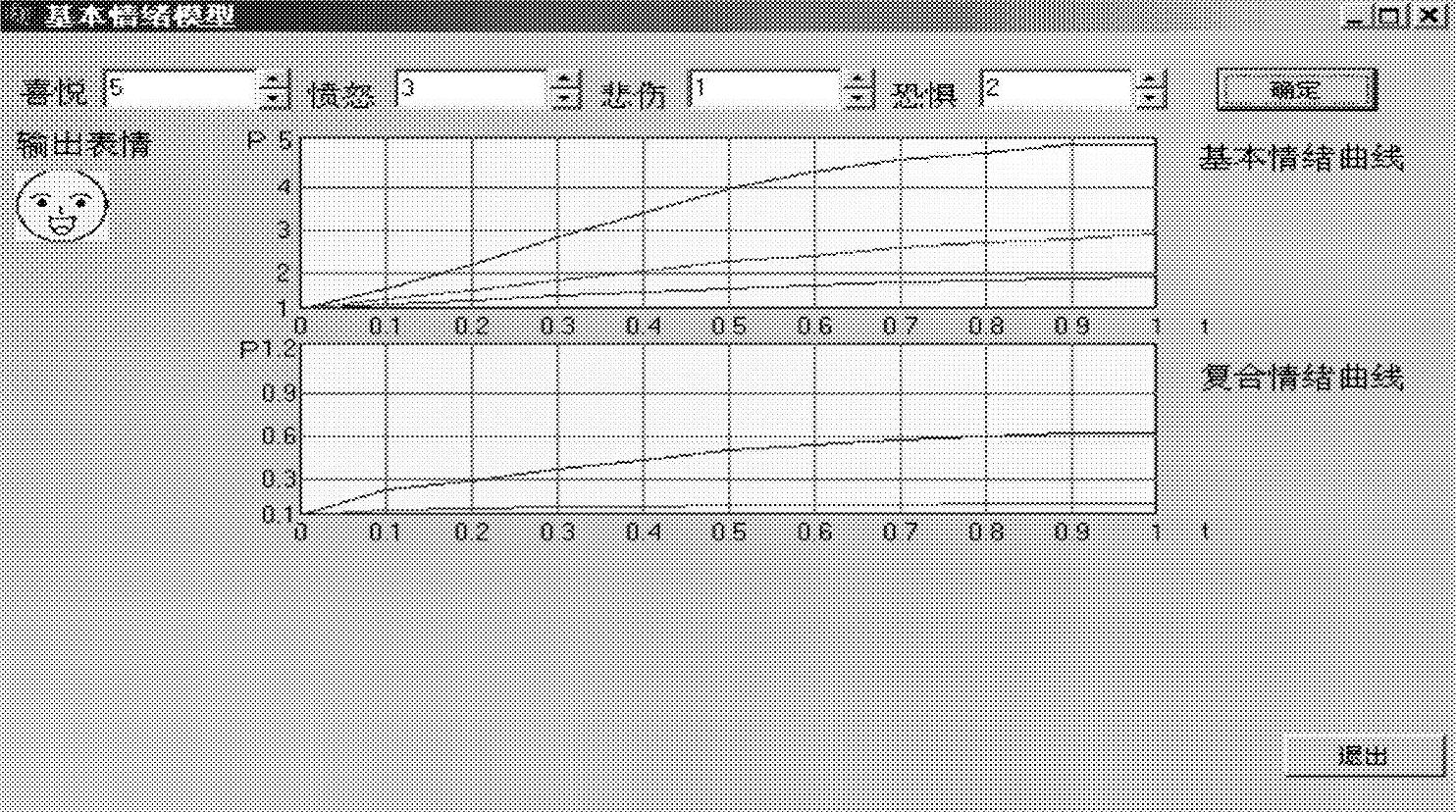
图3-35 接受刺激模型仿真界面
界面的组成部分包括:
刺激的输入。根据图3-5所示的表情种类,该仿真只模拟了四种基本情绪的情况。在仿真界面最上方的四个基本情绪输入框中输入刺激强度。
基本情绪输出曲线。根据基本情绪方程,随着时间参数t的改变,实时地输出对应于时间t的各基本情绪的曲线。
复合情绪曲线。由基本情绪和内驱力的结合,随着时间参数t的改变,实时地输出对应于时间t的各复合情绪分量的曲线。
输出表情。在基本情绪曲线左边,实时地根据复合情绪将对应的表情输出。
图3-36所示为无刺激输入模型仿真界面,它是在图3-35所示仿真的基础上,在情绪已稳定的情况下,增加了情绪向平静转移的曲线输出。该输出曲线有两个参数:时间参数t和情绪熵的负值参数(由于在模拟退火算法中采用了熵的负值作为目标函数)。由恢复平静曲线可看出,在无外界刺激的情况下,随着时间t的改变,情绪熵的负值一直在减少,所以情绪熵一直在增加。在熵值最大时,情绪达到平静状态。但由于退火算法中不断给予目标函数微小扰动,所以熵值不会稳定在某一固定值,而是围绕与平静时刻对应的固定值上下波动,既不会远离,也不会无限趋于该值。这与理论上推导出的结果是相一致的。
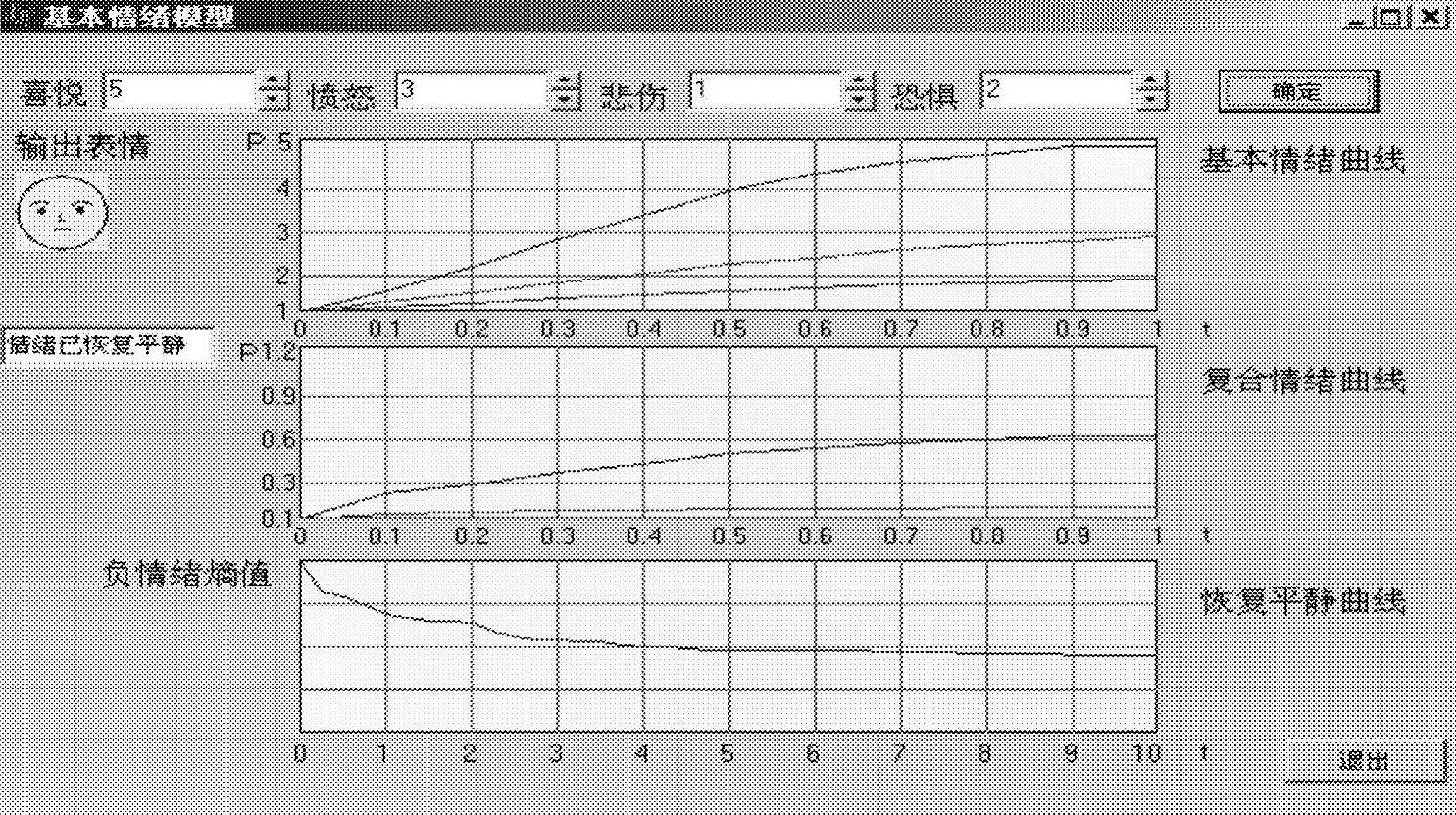
图3-36 无刺激输入模型仿真界面
(3)结论 该模型在基本情绪理论的基础上,建立了一套心理模型,进而给出了该理论的一套数学描述及其推导,其目的在于对情感状态的变化进行数学描述,对情感的变化规律进行表达,并给出了近似求解的数值算法。
通过仿真,可以直观地看到所模拟的情感变化过程,并可根据调整参数(B、α、β)来修改曲线,以使曲线更好地与实际相符合。
该模型中所做的这些工作,都是试图建立一个表现结果接近与人类的情感模型,为情感机器人的数学建模与情感决策支持系统提供了一种新的方法。
4.基于马尔可夫过程的情绪状态转移模型
该模型提出的情绪模型的基本思想是:认为人类情绪在不同状态间的转移是一个马尔可夫过程,其转移概率矩阵可以通过统计学的方法加以确定。该模型还依据心理学的理论提出了一种设计调查问卷的方法,以获取数据确定一般人的情绪状态转移概率,并给出了一套符合统计学理论的数据处理方法。
(1)该模型的构造
1)情绪状态集:对情绪变化过程建模必然涉及对情绪分类的问题。有些学者更关心连续情感状态的分布。然而Picard教授指出:那些喜欢将情感当作连续量的人,可以考虑离散的分类是连续空间的一个区域。从某种意义上说,选择离散或连续状态就好像用粒子或波动来描述光一样。最终,哪一种解释更好,取决于你要解释什么问题。基本情绪理论认为,情绪在发生上有原型形式,即存在着数种泛人类的基本情绪类型,每种类型各有其独特的体验特性、生理唤醒模式和外显模式,其不同形式的组合形成了所有的人类情绪。因此,该模型将k种基本情绪作为独立的情绪状态从而构成情绪状态集S,S={1,2,…,k}。
2)决策:情绪理论认为:认知将当前环境信息转变为中枢神经信号,对将来的环境变化产生预测,最终促使生命体产生适应性行为。这种对外界刺激的认知行为,是生命体适应生存环境的本能手段。生命体产生什么样情绪感受(是忧虑还是期待),以及什么样情绪反应(是进攻还是逃跑),都基于对当前刺激可能产生的结果的某种预测之上。因此,模型用随机变量ai反映生命体的上述本能的认知行为,i表示当前时刻正处于第i种情绪状态,称ai为决策。
3)决策与情绪状态转移概率的关系:在目前时刻处于第i种情绪状态,采取决策ai,则到下一时刻转移到第j种情绪状态的概率用pij(ai)表示。在自然现象中,大量随机变量都服从或近似服从正态分布。因此,该模型认为当前时刻处于第i种情绪状态的不同的人,在有外界刺激条件下的决策ai~N(0,σ2i)。
hn=(i0,a0,i1,a1,…,in-1,an-1,in)称为历史。策略π指序列π=(π0,π1,…),当历史为hn时,策略按ai上的分布π(·|hn)采取决策。
如果π(·|hn)与时刻n无关,称之为随机平稳策略。L(π)表示序列(X0,Δ0,X1,Δ1,…),Xi表示时刻i时的状态,Δi表示时刻i时的决策。
容易猜想对于一般的策略π,L(π)不是一个马尔可夫链,当π是平稳策略时,L(π)是一个马尔可夫链,且是时齐的。
证明:
由平稳策略的马尔可夫性及概率乘法公式知:
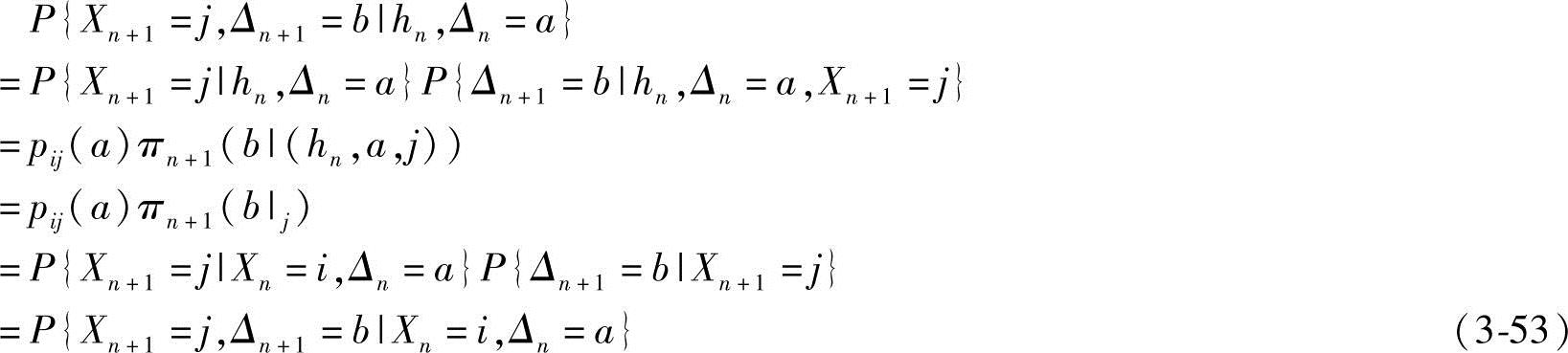
进而,L(π)的状态子序列Ls(π)是一个时齐马尔可夫链。
证明:对于Ls(π),由全概率公式及平稳策略的定义知:
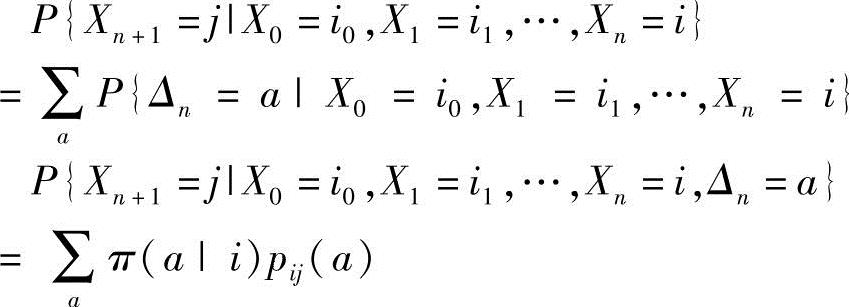

转移概率矩阵为

式中,pij=P{Xn+1=j|Xn=i}。
将情绪状态转移概率矩阵第i行的元素按大小重新排列,用p′ij表示(p′i1≥p′i2…≥p′ik)。考虑到ai~N(0,σ2i),可以将决策ai与情绪状态转移概率间的关系描述为
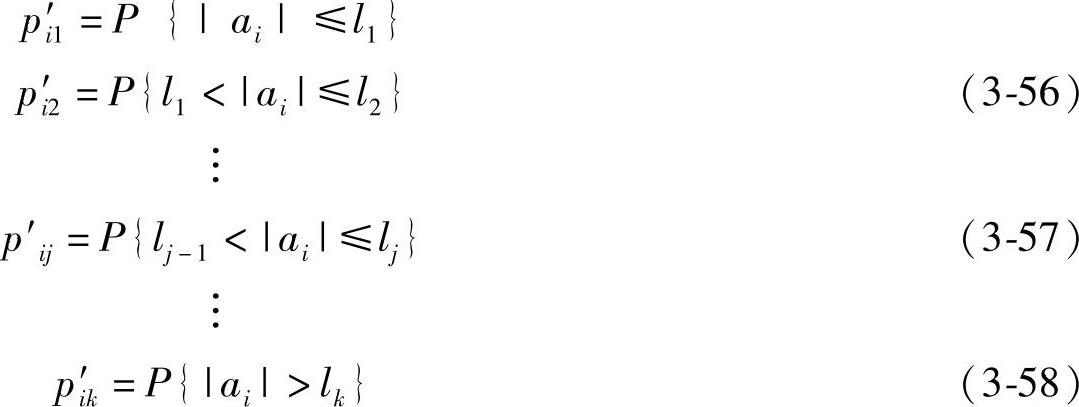
式中,lk>lk-1>…>l1>0,lj(j=1,2,…,k)表示ai所在区间的边界值。
4)报酬函数:情绪作为生命体适应生存的心理工具,其有效与否,取决于认知预测精确与否。该模型采用报酬函数作为认知行为精确与否的度量标准。取报酬函数r(i,ai)=1-exp(-lj),(j=1,2,…,k)。生命体采取的决策越精确,ai所在区间的边界值lj就越小,报酬函数的值也就越小。
(2)调查问卷 该模型的显著特点是可以通过调查问卷获得原始数据,再依据数理统计原理对数据进行处理,得到情绪状态转移概率。
1)调查问卷的设计方法:调查问卷属于主观体验测量方法。采用这种设计方法主要有两个原因。首先,各种以脑活动和外显行为为指标的研究方法,遗留的一个难以接触的方面是心理的“纯”主观方面的事物——例如体验。另外,无论生理或表情测量均需采用复杂的仪器。而且一般来说,不是一次性测量就能得出所需要的结果的。
该问卷将基本情绪区分为喜悦、悲伤、愤怒、恐惧、兴趣、厌恶六种。每一道问题都设计了被调查者在当前时刻所处的情绪状态,在这一时刻外界的刺激;各选项表示被调查者在题目设计的环境下将在下一时刻转移到何种情绪状态。根据基本情绪理论,情绪是指由特定刺激所激起的,由认知评价、主观感受、行为反应等因素组成的整个反应序列。因此,题目及其选项对情绪的描述不是仅限于情绪的主观感受,也包括与情绪相应的外显行为。
如何描述几种不同的基本情绪状态呢?普拉奇克建立了分别以功能语言、特质语言和行为语言来描述对应的术语。描述基本情绪使用了四种语言,见表3-5。
表3-5 描述基本情绪的四种语言

(续)
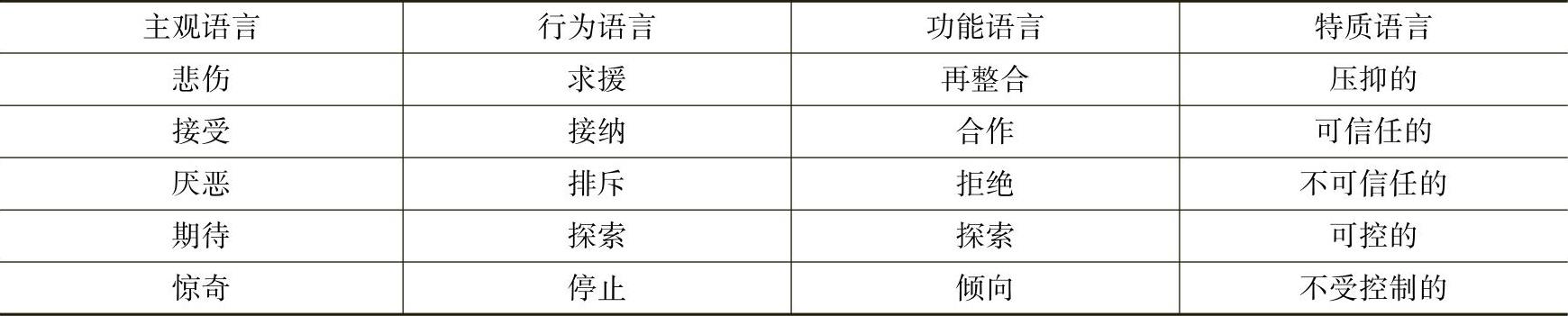
该模型参考普拉契克的用形容词描述情绪的办法,设计了调查问卷。
例题:你的一项工作办砸了,你心情忐忑不安,这时你的领导当众批评你,你会:
A.认为领导的批评不合理,对领导的做法不满
B.自己也在埋怨自己,心情郁闷
C.是预料之中的事,心里反而平静了一些
D.担心领导会对自己失去信任
E.同意领导的观点,冷静地分析自己的失误
F.认为领导伤了自己的脸面,对他很反感
2)数据的处理方法:将问卷得到的数据按数理统计方法处理,求得一般人的情绪状态转移概率。
将所有人从第i种情绪状态转移到第j种情绪状态的概率值的全体称之为总体Xij。设有k种基本情绪状态,要研究的总体数量就是情绪状态转移概率矩阵的元素数k×k。每个人从第i种情绪状态转移到第j种情绪状态的概率值称为总体Xij的个体。
按照题目设定的被调查者在当前时刻所处的情绪状态,对题目进行分类。因为有k种基本情绪状态,所有题目分为k类。每类题目设定的被调查者在当前时刻所处的情绪状态相同。对每一类题目:
首先,统计其包含的题目数量,记为Si下标i表示该类题目设定被调查者在当前时刻处在第i种情绪状态。
然后,分别统计与被调查者选择的选项对应的他在下一时刻转移到各种情绪状态的数量,记为Tj,下标j表示被调查者在下一时刻将转移到第j种情绪状态。
最后,计算被调查者的情绪状态转移概率pij:

对某类题目的调查结果做上述处理,就能得到从该类题目设定的被调查者在当前时刻所处的情绪状态向各个情绪状态转移的概率,这些概率构成了情绪转移概率矩阵的一行。依次处理各类题目相应的调查结果,最终得到一个被调查者的情绪状态转移概率矩阵P为

对n份问卷的调查结果进行上述处理,就得到了对各个总体Xij的n个观察结果,n称为这个样本的容量。
该模型中,认为所有人从第i种情绪状态转移到第j种情绪状态的概率这一总体Xij服从正态分布。设计本问卷目的是,确定符合一般人的标准情绪状态转移概率矩阵。标准情绪状态转移概率矩阵的意义是:绝大部分人的情绪转移概率值在它的元素值附近波动。服从正态分布的随机变量的概率密度随着随机变量与分布函数均值的距离增加而减小,当随机变量接近均值时,其概率密度很大。该模型根据正态分布函数的这个特点和标准情绪转移概率的意义,把总体Xij(i,j=1,2,…,k)的分布函数的均值μij作为相应的标准情绪转移概率值pij。
取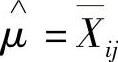 、
、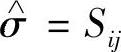 ,如果X~N(μ,σ2),对于随机变量X来说,它的值落在区间[μ-3σ,μ+3σ]内,几乎是肯定的事。因此,将问卷中得到的落在区间
,如果X~N(μ,σ2),对于随机变量X来说,它的值落在区间[μ-3σ,μ+3σ]内,几乎是肯定的事。因此,将问卷中得到的落在区间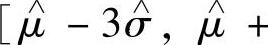
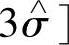 之外的样本值视为异常样本值。在剔除异常样本值之后,依据正常的样本值对总体分布函数的μ和σ2重新进行点估计。
之外的样本值视为异常样本值。在剔除异常样本值之后,依据正常的样本值对总体分布函数的μ和σ2重新进行点估计。
下一步,对总体分布函数的均值μ进行区间估计。根据数理统计的知识,得到μ的置信度为1-α的置信区间:

式中,n为样本容量;S为样本方差;t为学生氏分布。对于标准转移概率矩阵P有
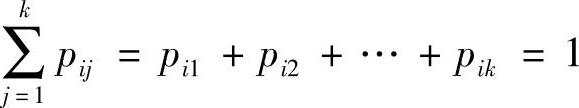
由于,标准的情绪转移概率是所有人的情绪转移概率的总体的均值,那么
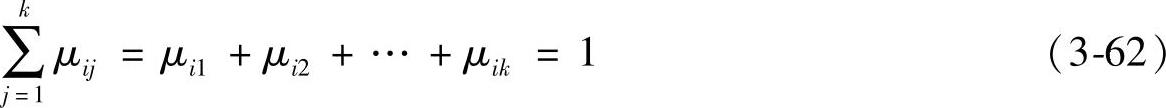
式中,μij表示所有人从第i种基本情绪转移到第j种基本情绪的概率的总体Xij的均值∀i,求出μij(j=1,2,…,k)满足上述方程的解。
可以采用遗传算法搜索上述方程的解,将解的搜索范围限制在μij的置信区间内。遗传算法的关键问题是确定适应度函数。本模型取适应度函数为

假设上述方程的解是各个情绪转移概率的总体的均值,分别进行假设检验。
设Xij~N(μij,σ2ij),其中μij、σ2ij为未知,我们来求检验问题

的拒绝域(显著性水平为α)。若Xij为样本均值,S2ij为样本方差,则拒绝域为
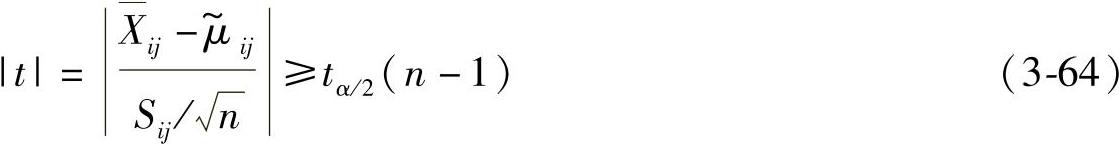
经假设检验,若t不落在拒绝域中,就接受H0,即认为总体Xij的均值为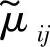 ;否则,认为
;否则,认为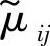 不是总体Xij的均值,需要利用方程重新搜索Xij的均值的解。
不是总体Xij的均值,需要利用方程重新搜索Xij的均值的解。
(3)结论 该模型力图反映在有外界刺激的条件下,一般人的标准情绪变化过程。与其他情绪模型相比,它有如下特点:①考虑了外界刺激对人类情绪变化过程的影响;②采用调查问卷的方法,获得数据;然后依据数理统计原理确定情绪状态转移概率;③得到的情绪转移概率矩阵反映的是人类一般的情绪转移概率。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






