1.普拉奇克的情绪锥球

普拉奇克（R.Plutchik）所提出的情绪锥球描述如图3-9所示。这种方法混合了维度和基本情绪理论。他认为任何情绪的相近程度都有不同，任何情绪都有与其在性质上相对立的另一种情绪，任何情绪都有不同的强度。他采用强度、相似性和两极性三个维量，并用一个倒立的锥体，在锥体切面上分隔为块，切面上的每一块代表一种原始情绪。共有8种原始情绪，每种原始情绪都随自下而上强度的增大而有不同的形式；截面上处于相邻位置的情绪是相似的，处于对角位置的情绪是相对立的；截面中心区域表示冲突，是由混合的动机卷入而形成的。普拉奇克认为，所有情绪都表现出强度的不同，如从忧郁到悲痛；任何情绪在与其他情绪相似的程度上都有不同，如憎恨与愤怒比厌恶与惊奇更为相似；任何情绪都有相对立的两极，如憎恨与接受，愉快与悲伤。

2.普拉奇克情绪圆环模型（见图3-10）

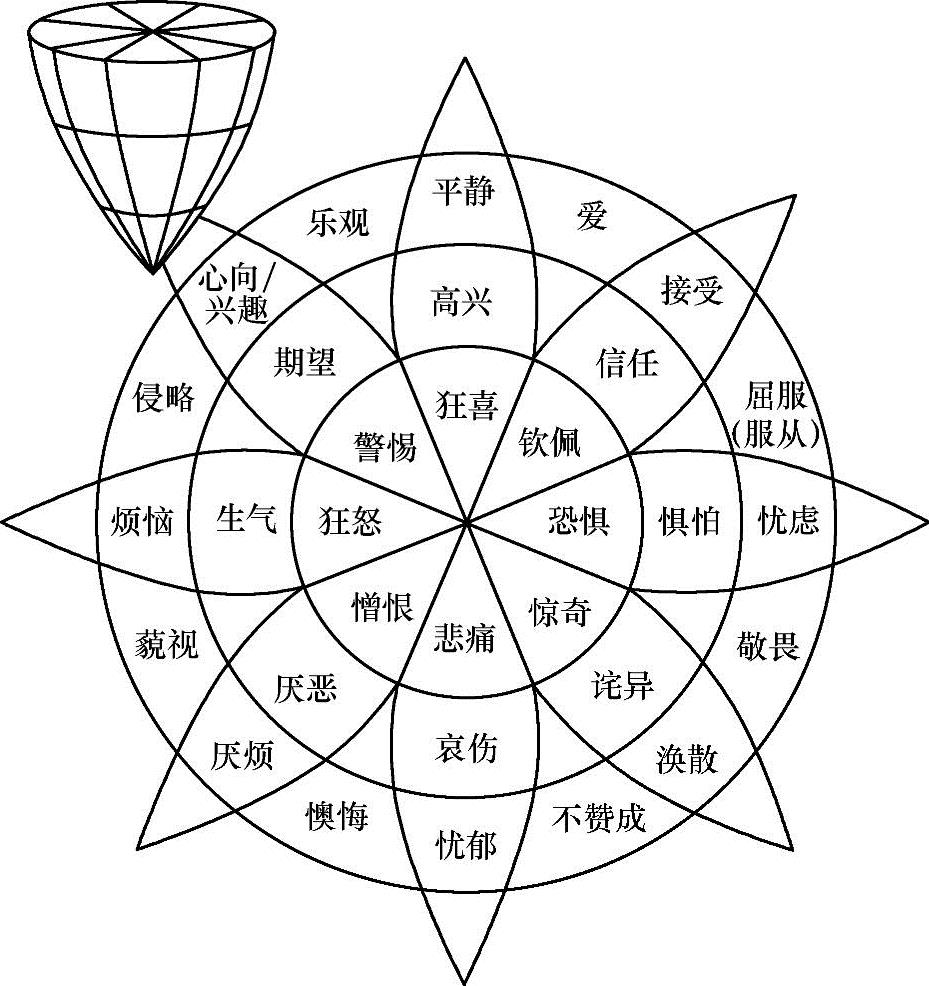
图3-9 普拉奇克的情绪锥球模型

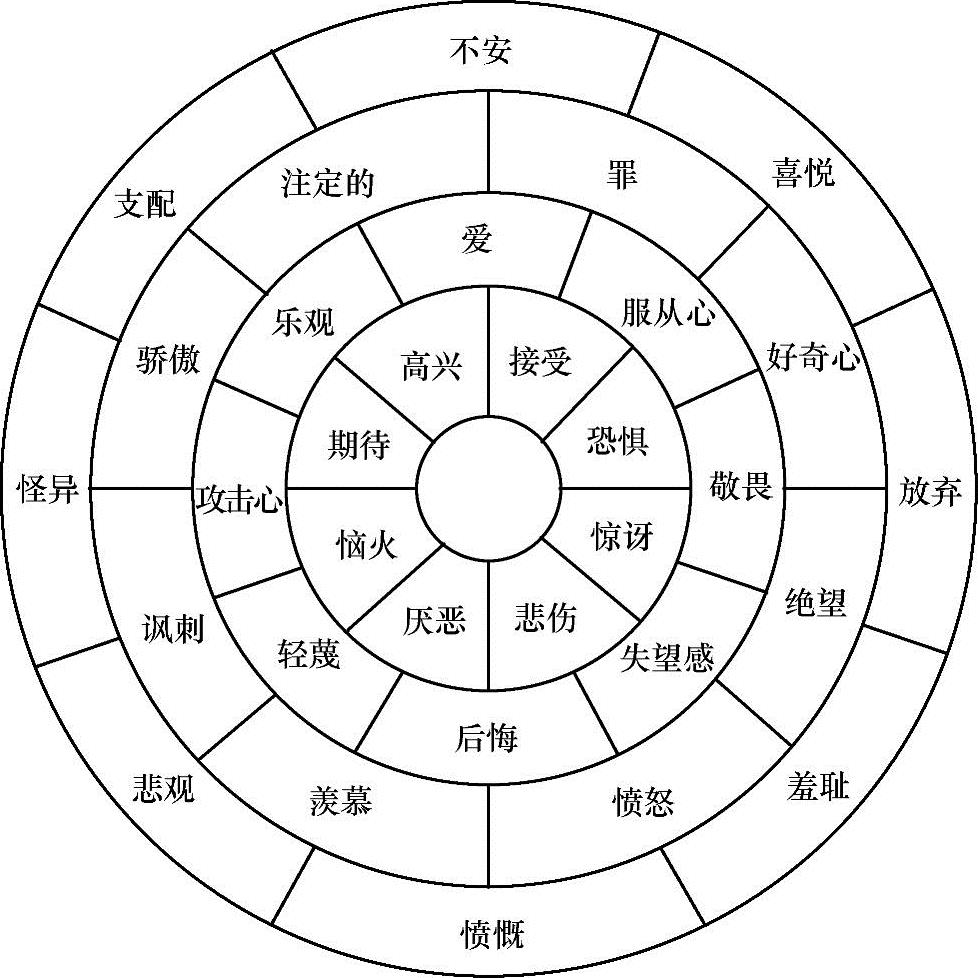
图3-10 普拉奇克情绪圆环模型

3.鲁塞尔（Russell）的情感圆环模型（见图3-11）(www.daowen.com)

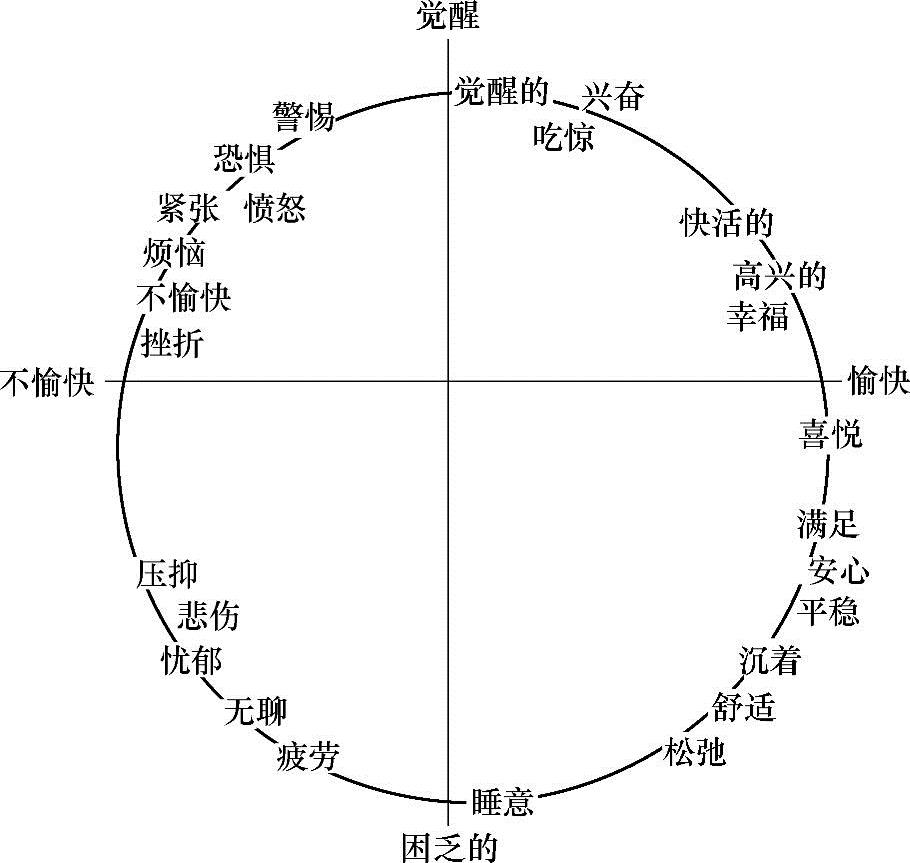
图3-11 Russell的情感圆环模型

4.拉森（Larsen）和迪恩尔（Diener）八方向模型（见图3-12）

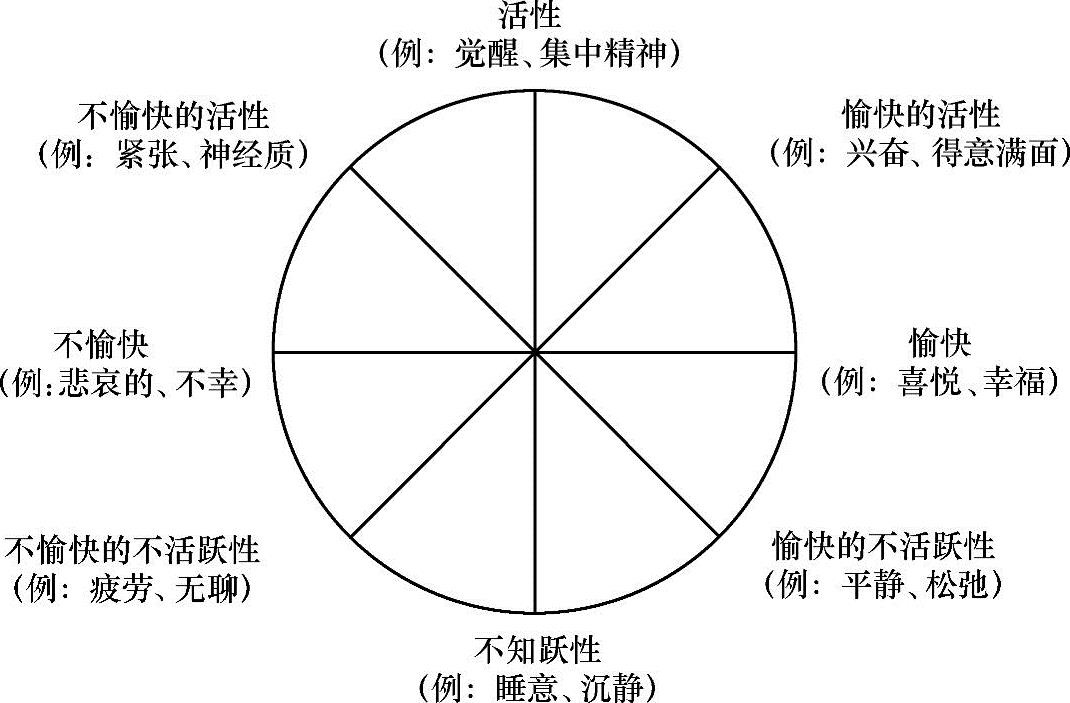
图3-12 Larsen和Diener八方向模型

5.情绪的方锥空间模型（见图3-13）