前述短时间冲击作用的结构反应，是以特定形态的脉冲型击波为动荷载，其计算方法有一定局限性。现在讨论一般的任意动荷载p（t），是时间t的任意函数，在t=τ时刻的荷载大小为p（t），在很小的时间间隔Δτ内，则p（τ）dτ是短时间的冲量，已知方程式（7-42）可用来计算这个冲量的反应，不过这是个近似的方法。当dτ→0时，为精确的方法。

在时间Δτ内荷载p （τ）引起的结构反应则为

对一个任意P（t）的荷载，如图7-9所示，整个荷载时间过程可以看作一列离散的短时脉冲作用所产生反应的总和。每一个脉冲反应如式（7-44）所示的微小反应，则总反应就是将荷载时程的全部微小反应相加而得，即对式（7-44）进行积分：

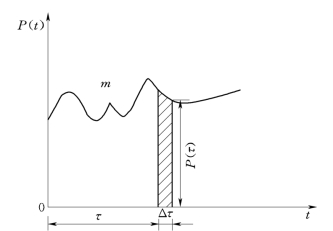
图7-9　任意动荷载

这是无阻尼的动力荷载的反应的Duhamel积分表达式。

作为一个例子，假定P（t）=P0（0≤t≤t1），方程式（7-45）则为

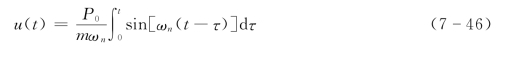
积分结果显然有

(www.daowen.com)

或者

由式（7-48）可见，最大位移为um时，cosωnt= -1，有

这就是前述矩形突加脉冲击波的结果。可见，由Duhamel积分计算动力反应更为方便。

通常实际的结构物都是有阻尼的。推导方法与上述无阻尼的相同，不同之处仅指p（τ）dτ引起的反应按指数衰减，因此方程为

对整个荷载作用时间内积分，可求出位移反应为

式中：ωd为有阻尼的圆周率；ξ为阻尼比。

式 （7-47）就是有阻尼的Duhamel积分方程。

一般情况下，由于P（t）不是一个简单函数，因此，不可能用解释的办法求出积分，实际工程问题都是采用数值积分方法。这方面有专门的计算机程序可供选用。