（1）运动方程。多质点系以速度位移激励的非线性动力反应方程，用矩阵形式写出较为简便：

t+Δt时刻的运动方程与式（6-193）类似，只需将式中的t改为 （t+Δt）即可，于是由两式之差，得增量方程为

式中

以下讨论求解非线性平衡方程的数值方法。

（2）等加速度法。与单质点系一样，取时间步长初值的加速度为该步长Δt的加速度值，即在时间间隔Δt内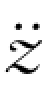｛（t）｝=常数，于是t+Δt时刻的绝对位移、绝对速度为

将式（6-196）和式（6-197）两式代入方程式 （6-194），即t+Δt时刻的非线性动力平衡方程，求t+Δt时刻的绝对加速度为

相对位移和相对速度则用式（6-199）求出：

相对位移和相对速度仍用式（6-199）求出。

（4）速度、位移激励的增量方程解非线性多自由度运动方程的线性加速度法

与前述单自由度方法类似。

将两式代入增量平衡方程式（6-194）解出｛Δz（t）｝为

式中

重复以上步骤可逐步求出每一步长的绝对位移、绝对速度、绝对加速度反应。而相对位移、相对速度反应由式（6-209）求得：

（5）速度位移激励的增量方程解非线性多自由度运动方程的Wilson—θ法。(www.daowen.com)

类似于单自由度的计算方法、步骤，在τ=θΔt时刻的反应量为

又将式（6-212）代入式（6-211）得

式中

相对位移与相对速度则为

逐次重复以上步骤，可得动力反应全过程。

（6）速度位移激励的增量方程解非线性多自由度的运动方程Newmark法。

Newmark方法的基本公式为

这时有

式中

[I]为单位对角矩阵。

然后求t+Δt时刻的绝对位移、绝对速度和绝对加速度，仍然是用式 （6-220）、式（6-221）和式（6-222）。

相对位移与相对速度则用式（6-223）求出。

重复以上步骤，逐步计算各步长的反应，即可得全过程的响应。