速度位移激励的非线性单自由度的动力反应，其动力平衡方程仍采用增量形式表示，在时刻t的方程为

t+Δt时刻的则为

式 （6-151）和式（6-152）中的刚度k（t）、阻尼系数c（t）均是时间的函数，右端项是速度和位移激励产生的作用，二者相减用增量表示的加速度、速度与位移为

这里假定在Δt很小的情况下，刚度、阻尼变化不大，则近似有

于是得速度位移激励的增量平衡方程为

对于单自由度系统，可以将式（6-154）中k（t）和c（t）用频率与阻尼比表示，则有

以下讨论求解上述方程的数值方程。

（1）非线性体系的线性加速度法。

根据加速度为线性变化的假定，在时段末t+Δt时刻速度与位移表达式和时段初t时刻速度与位移表达式可求出增量表达式为

将式（6-158）及式（6-159）代入增量动力平衡方程式（6-155），就可得出Δz（t）的解答式为

式中

将式（6-161）代入非线运动平衡方程式（6-152）求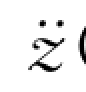（t+Δt），即

或表达为

相对位移、相对速度、相对加速度可用式（6-164）～式 （6-166）求出：

一般情况，对于爆破来说可以不求相对加速度。

现将以速度和位移激励的非线性单质点体系动力反应数值法（加速度线性变化）求解的步骤归纳和下：

1）由式（6-160）求t时刻绝对位移增量Δz（t）。

2）用式（6-161）计算t+Δt时刻的绝对位移、绝对速度。

3）用式（6-163）求t+Δt时刻的绝对加速度。(www.daowen.com)

4）以t+Δt时刻的z（t+Δt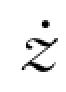）、（t+Δt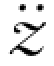）、（t+Δt）为初始值，重复前述1）～3）步，直到全部计算完成，求出以爆破地震的速度和位移激励的非线性单自由度体系的振动反应全过程。

（2）Wilson—θ法求速度位移激励非线性单自由度体系的动力反应。

Wilson—θ法，仍是假定加速度为线性变化，它的求解方法与第6.1.3 （5）节相类似，这里可以根据其思路，用速度位移激励的增量方程导出求解公式。现直接写出其计算步骤与相应的计算公式：

1）以时刻t+Δt加速度线性变化，导出：

解出Δzτ（t）为

式中

其中

5）由式（6-161）求t+Δt时刻的位移和速度：

t+Δt时刻的相对速度与相对位移则由式（6-179）求出：

6）重复上述步骤，可求出非线性反应的全过程。

（3）Newmark法增量方程求速度位移激励非线性单自由度体系的动力反应。

设t+Δt时刻的运动量与t时刻运动量之差为增量，则

于是由上述关系式可得

再代入到式（6-183）可得

将式（6-185）、式 （6-186）代入增量方程式 （6-154）或式 （6-155）可求得Δz（t）为

式中

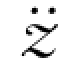（t+Δt）由t+Δt时刻的动力平衡方程求出为

重复以上过程可求得整个时程反应。