（1）多质点系运动方程。多质点非线性体系的运动方程，与单质点系不同之处是他们构成了一组运动平衡方程，通常用矩阵形式写出比较简练。地震动作用下的多质点系平衡方程为

受任意动荷载作用的方程可写为

用 [M]除两边，则

R（t）可以是冲击作用在结构上的荷载，也可以是运动引起的结构惯性力。

在天然或人工爆破地震作用下：

以下讨论多质点非线性体系的数值法求解时程反应。由于各方法均与单质点体系类似，因此，一般仅列出结果，而不作详细推导与证明。

（2）等加速度法。这一方法假设在时间间隔内加速度为不变化的常数，即｛ü（t）｝为常数，于是t+Δt时刻的位移和速度可表示为

将两式代入方程式 （6-70）或式 （6-71），即代入非线性动力平衡方程，求t+Δt时刻的加速度为

重复利用式（6-73）～式 （6-75）三式，可求得多质系的动力反应的全过程，即时程反应。

（3）中点加速度法。取时间间隔Δt内的中间点，即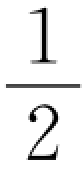Δt时间处的加速度为该步长的加速度的值，再按前述的等加速度方法求算。

1）求算中点位移和速度值。

重复1）～3）步，逐次求出各时间间隔末的位移、速度和加速度值。

（4）线性变化加速度法。

假设在时间间隔Δt内，｛ü（t）｝为线性变化，则相应t+Δt时刻的位移、速度则可表示为

这里仍用增量法求解，用增量表示的运动方程为

式中

根据上述增量关系，由式（6-81）和式（6-82）可求得增量为

由式（6-84）解出｛ü（t）｝为

代入式（6-85）有(www.daowen.com)

将式（6-86）及式（6-87）中的｛Δü（t）｝、｛Δu·（t）｝代入增量动力平衡方程式 （6 83）中，可求出位移增量｛Δu（t）｝为

式中

用式（6-88）解出｛Δu（t）｝后，就可由式（6-87）求出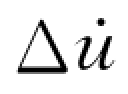｛（t）｝，然后用步长内增量的关系式求出t+Δt时刻的位移和速度值为

代入动力平衡方程可计算出ü（t+Δt）为

将t+Δt时刻的值作为下一步的初始值，逐次求出新的步长末的反应量，从而可求得动力全过程的反应。

这种方法是有条件稳定的，要求足够小的步长Δt，否则有可能导致不稳定。

（5）Wilson—θ法。Wilson—θ法是无条件稳定的线性加速度法，即只需要θ≥1.37就是稳定的。因此它的计算仍可用前述增量法的思路求解。Wilson—θ法是先求t+Δt时间间隔的增量Δu（t+θΔt）（为表述简化，常用τ表示θΔt），求出t+τ时刻的结果，再求t+Δt时间的反应量。

根据6.1.4节中（4）的做法，在式（6-84）、式 （6-85）中用τ代替Δt，则有

以｛Δu（t）｝为变量，由式（6-94）解出增量｛Δü（t）｝为

求出｛Δu（t）｝后，因为这里相当于t到t+τ时刻的位移增量，因此应由式 （6-96）求出相应t+τ的｛Δü（t）｝，再除以θ，即可得相应t+Δt的增量｛Δü（t）｝，即

重复以上计算过程，可求得全过程的反应。

（6）Newmark法。Newmark法是在线性加速度法的假设下，引入两个参数α及β，得到了广泛应用的方法。

该方法的基本公式为

如单自由度一样，α宜取1/2，否则将产生 “伪阻尼”，α＜1/2时，伪阻尼取负值，α＞1/2时，伪阻尼取正值。伪阻尼的值与（α-1/2）成正比，因此Newmark建议α=1/2。

β的取值对方法的稳定性有影响，研究表明，β=1/4时，为无条件稳定法，而且计算精度也较好。还应注意到，β=1/4，当Newmark法就变为中点加速度法；β=1/6时，为线性加速度法；β=1/8时，在Δt内，加速度为阶形变化。一般β取值在1/4～1/8之间。用增量形式求解，这时有

式中

由式（6-106）求出｛Δu（t）｝之后，按式（6-10）计算｛Δ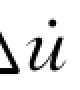（t）｝有

然后，求t+Δt时刻的位移、速度及加速度，仍用式 （6-91）、式 （6-92）和式（6-93）。重复以上过程，可求出全过程的反应，即时程响应。