（1）荷载作用与构件材料变形的关系。弹性体系振动问题的数值积分法不适用于弹塑性体系，弹塑性性质表明力与变形关系是非线性的，体系的阻尼、刚度都是时间的函数，只有结构的质量还可以当作常量处理。

结构在受强烈地震动作用下，其恢复力与变形的非线性关系是复杂的，通常都是以分段线性化的关系来替代，即用折线代替曲线。

对一个弹塑性非线性体系进行动力分析时，必须建立荷载变形之间的关系，并用理想化的数学关系来描述，就是所谓的恢复力模型。

材料应力应变关系为非线性的称为材料非线性，对作用力与大变形的非线性称为大变形非线性。这些都可用数值积分法计算地震动的非线性时程响应。

（2）单质点非线性 （弹塑性）体系的运动方程。非线性的弹塑性体系，材料的变形（或结构的变位）与刚度的关系是非线性的，即刚度k是时间的函数，用k（t）表示，k（t）随变形u（t）而变；阻尼c也是时间的函数随变形速度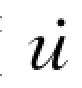（t）而变，用c（t）表示；质量为常数，仍用m表示。这样，单质点系的弹塑性运动方程，即可表示为

对于受地震动作用的非线性单质点系运动方程可表示为

üg（t）为爆破地震动加速度记录时程曲线。

由于单质点系的自振频率是k（t）和m的函数，根据弹性关系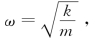则弹塑性单自由度体系的频率也是时间的函数，即

相应的阻尼则也为时间的函数，即

显然阻尼比ζ（t）也是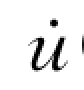（t）的函数。

引入ω（t）和ζ（t），将式（6-29）进行变换，非线性单自由度体系运动方程亦可写成

（3）单自由度非线性体系运动方程的解法概述

将方程式（6-28）、式 （6-29）和式（6-32）与线弹性单自由度的动力平衡方程相比较，形式上是相似的，只是将线性的方程中的常数ω、ζ换成随时间而变的ω（t）与ζ（t），或将常数k、c换成随时间变化的k（t）、c（t），因此，求解的难度就在于如何确定k（t）和c（t）。假定材料的非线性刚度k（t）由曲线切线斜率表示，如图6-4 （a）所示。

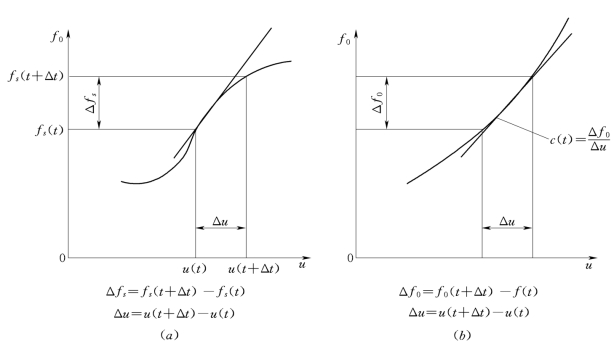
图6-4　材料非线性刚度及阻尼

（a）刚度k（t）；（b）阻尼c（t）

阻尼系数c（t）由阻尼力与变形关系曲线确定，如图6-4 （b）所示。由于质量m为常数，已知t时刻的变形为u（t），变形速度为u·（t），于是t时刻的ω（t）与ζ（t）均可求得，代入相应于求线性体系中的动力反应各逐步积分式，就可求出t+Δt时刻的反应，然后依据 （t+Δt）时刻的k（t+Δt）、c（t+Δt），确定ω（t+Δt）与ζ（t+Δt），又可逐步求出下一步的反应。如此逐步递推，直至地震动时间全过程结束。

原则上讲，线性问题的各种逐步积分法，都可用本办法求非线性问题，但是在实际应用时，由于材料、结构非线性在加载、卸载过程中的非线性路径是不一样的，而且结构振动时加载卸载变化十分频繁，不可能由单一的力～变形关系曲线u（t）～fs（或f0）确定。实际应用必须给出所研究的结构物或结构体恢复力模型，即建立构件所受荷载与其变形之间的关系曲线，并理想化后用数学关系或几何关系表示。

大量试验研究表明，应变滞后于应力，因此力～变形关系曲线总具有滞回性质，即形成滞回环。滞回曲线的形状、滞回环的面积、大小与许多因素有关，可以参阅关于这方面的研究成果和著作。

（4）增量方程式求非线性单自由度体系的动力反应。这种方法的思想是求时间间隔Δt内的位移、速度与加速度的增量Δu（t）、Δu·（t）、Δü（t），然后与该时刻t的初始值u（t）相加，即可得t+Δt时刻的值，而求增量的方法仍采用线性加速度方法，分别列出t及t+Δt时刻的非线性单自由度体系的运动方程，以式 （6-28）为例，t时刻的非线性单自由度体系的运动方程为

t+Δt时刻的非线性单自由度体系的运动方程为

由式（6-34）减去式（6-33），并认为t时刻的阻尼及刚度系数相等，即c（t+Δt）≈c（t），k（t+Δt）≈k（t），于是得到

式中

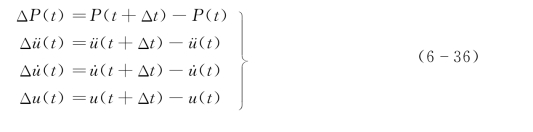
这就是增量方程。

增量方程中的Δü（t）、Δ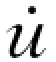（t）、Δu（t）相当于动力平衡方程的加速度变量、速度变量和位移变量，根据线性加速度的假设，按照本章 （2）中的方法进行推导，将式 （6-8）及式（6-9）变换为

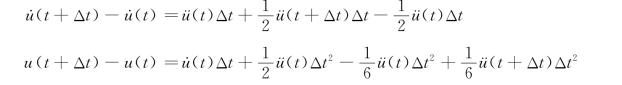
用增量来进行表示有

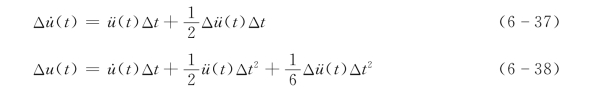
由式（6-38）解出Δü（t），有

将式（6-39）代入式（6-37）得

将式（6-39）及式（6-40）代入增量动力平衡方程式 （6-35）可得到关于增量Δu（t）的解答式为

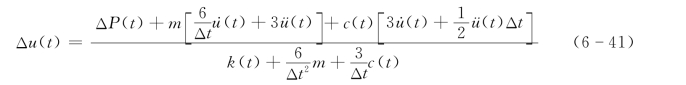
把上式右端的分母写成k*（t），分子写成ΔP*（t），分别称为等效刚度和等效荷载，其解法完全类同于静力法，即位移增量Δu（t）等价于ΔP*（t），除以k*（t），故亦称拟静力法。

由式（6-42）或式（6-41）求出u（t）后，再由式（6-37）求速度增量Δu·（t），然后求t+Δt时刻的位移和速度，即(www.daowen.com)

t+Δt时刻的加速度ü（t+Δt），则由运动方程式（6-28）求出，即用式（6-43）算出的结果代入式（6-28），可求得ü（t+Δt）为

由此可见，用线性加速度假定求单自由度非线性体系或弹塑性体系动力响应的增量法的步骤已得出，用递推法，可继续求出下一个步长的振动量。现将计算过程归纳如下：

1）由该步长的初始值（前一步长的末端值）求该步长的位移增量，即用式 （6-41）计算Δu（t）。

2）由式（6-43）计算本步长的位移u（t+Δt）和速度u·（t+Δt）。

3）由式（6-44）计算ü（t+Δt）。

4）重复以上步骤，即将本步长u（t+Δt）、u·（t+Δt）、ü（t+Δt）作为下一步的初值，递推求出整个动力反应过程。

为了应用方便，仍写出以方程式 （6-32）的计算求解公式，式中üg（t）为地面运动加速度，ζ（t）、ω（t）为t时刻的阻尼比及圆频率。事实上，只要在上述有关计算公式中，将k（t）用mω2（t）代替，c（t）用2ζ（t）mω（t）代替，p（t）用müg（t）代替或ΔP（t）用Δüg（t）代替，加以整理后，即可得出求解式（6-32）的递推公式，这里只写出其结果。

1）计算步长的位移增量Δu（t），由式（6-41）变换后得

2）计算t+Δt时刻的位移与速度，公式同式（6-43）。

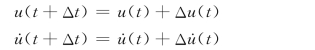
3）计算t+Δt时刻的加速度，由式（6-44）变换后得

ü（t+Δt）=-üg（t+Δt）-ω2（t+Δt）u（t+Δt）-2ζ（t+Δt）ω（t+Δt）ü（t+Δt）

4）以t+Δt时刻的位移、速度、加速度为初值，重复以上步骤，直到全过程计算完毕，即可得出地震动加速度激励非线性单自由度体系振动的时程反应。

本方法是有条件稳定的，但当步长取得过大，计算结果将是发散的，因此选择步长应尽可能小一些。为此，Wilson提出一种无条件稳定的方法。下面介绍这一方法。

（5）Wilson—θ法的增量方程求非线性单自由度体系的动力反应

Wilson提出的无条件稳定的方法，即对步长没有限制，常称Wilson—θ法。基本要点是按（4）节增量法求对应于τ=θΔt的增量Δüτ（t），然后除以θ而得到对应于Δt的增量Δü（t）。其余计算步骤与（4）节线性加速度法相同。

Wilson证明当θ≥1.37时，是无条件稳定的。因为此方法是将Δt延伸到τ=θΔt，先求出τ时刻的结果，再由τ时刻结果推出Δt时刻的结果，与θΔt对应的增量只要在式（6-37）及式（6-38）中以θΔt代替Δt，即可求得

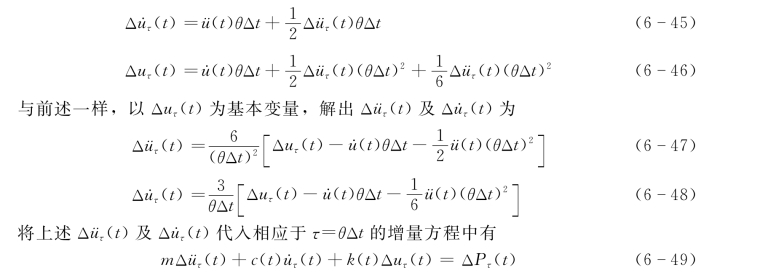
类同上一节可求得位移增量Δuτ（t）为

式中

用式（6-50）求出的Δuτ（t）代入式 （6-47）得到Δüτ（t），再除以θ，即得到对应于Δt的增量Δü（t），为

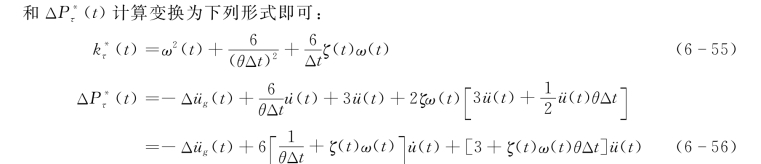
其余计算式与计算步骤均相同，即依次用式（6-50）、式 （6-54）、式 （6-37）、式（6-43）、式 （6-28）或式（6-44）各式完成计算。

（6）Newmark法的增量方程求非线性单自由度体系的动力反应

纽马克（Newmark）线性加速度法的基本公式和上述 （4）节方程式 （6-22）、式（6-23）相同，式中α=1/2。为了推导方便，下面写出它们为：

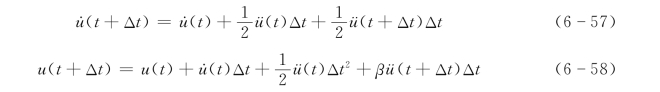
现将式（6-57）和式（6-58）二式改成增量形式，设

于是由式（6-57）、式 （6-58）得

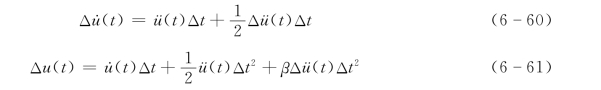
由式（6-61）解出Δü（t）有

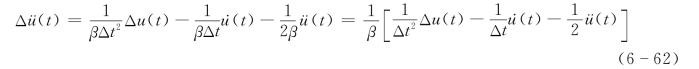
再代入式（6-60）得

将式（6-62）、式 （6-63）代入式（6-35），可得位移增量Δu（t）的解：

β值一旦确定，可求出ΔP*（t）及k*（t），Δu（t）则可由式（6-64）求出。如同前述一样，整个过程可重复上述计算步骤。

对于式（6-32）形式的动力平衡方程，只要改换平衡方程中的系数k（t）、c（t）及荷载P（t）的表示形式，即将式（6-65）及式（6-66）改写为

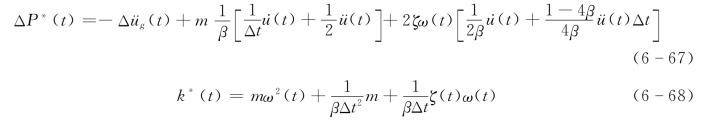
其他不变，整个求解过程也相同。