如前所述，单自由度线弹性体系的动力平衡方程通常写为下列三种形式：

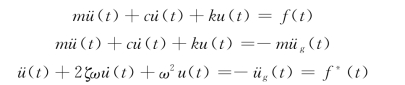
式中：f*（t）=f（t）/m；m、c、k依次为质量、阻尼与刚度；üg（t）为地面运动加速度；f（t）为外荷载。

本节介绍用逐步积分法直接求解单质点体系运动微分方程，推导出几种常用的数值解法的递推公式。数值解法的基本方法与步骤如下：

（1）将输入波的时间坐标离散为很小的步长Δt，Δt愈小，计算精度愈高，但计算工作量就越大。Δt的大小与结构自振周期、地震动波的频率或外加冲击动荷载作用时间等有关。

（2）对于线弹性体，质量m、阻尼c、刚度k与时间无关，整个动力反应过程中它们为常数。

（5）以前一个Δt的末端值作为下一个Δt的初始值，重复上述步骤，逐步递推计算下去，直到整个运动过程。

（1）常加速度法。常加速度法又称等加速度法，即是假定在每个时间步长Δt内加速度是常量，此常加速度取步长Δt两端的加速度平均值，如图6-1所示，而时段末的速度可推算出为

在时段末的位移则为

进行积分可得

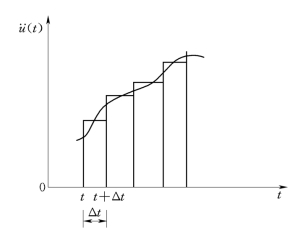
图6-1　常加速度法

这里，对于单自由度质点体系的运动方程可写为

将式（6-1）、式 （6-2）代入式（6-3）可求得时段Δt末的加速度递推公式为

（2）线性加速度法。线性加速度法，就是假定体系的加速度反应曲线在一段步长Δt内是线性变化，这实际上就是用分段直线连接成的折线来代表加速度曲线。在t～t+Δt时段内的加速度为

图6-2　线性加速度法

将式（6-5）对τ积分，得速度为

再对式（6-6）积分得位移为

若积分时间限为t～t+Δt，即τ=Δt，则由式（6-6）、式 （6-7）得该步长末的速度与位移，即

加速度ü（t+Δt），由式（6-3）来求得，即将式（6-8）和式 （6-9）代入式 （6-3），经整理运算后可得

在计算爆炸或爆破冲击波作用的结构动力反应时，由于冲击波作用时间短，特别是荷载的升压时间更短，计算步长也决定于冲击作用的有效时间，武汉长江科技有限公司有关人员曾对爆破地震情况的步长Δt选取进行过研究，得出Δt与有限元网格尺寸、结构材料常数等有关。

（3）Wilson—θ法。前面所述常加速度法和线性加速度法，是有条件稳定的方法。它的稳定性是由步长Δt的值决定的，当Δt大到某种程度（一般Δt＞0.55T）时，计算就不收敛，常称这种数值解法为条件不稳定的。为了克服这种现象，Wilson提出了一个有效的方法，这个方法通常称Wilson—θ法，它是无条件稳定的线性加速度法。

Wilson—θ法的基本要点是将Δt延伸到θΔt，θ=1就是线性加速度法。当θ≥1.37时是无条件稳定的，在θΔt时段内加速度呈线性变化。对于t+Δt时刻的加速度、速度和位移，只要将式（6-5）、式 （6-6）和式（6-7）中的τ用t+Δt代替即可得

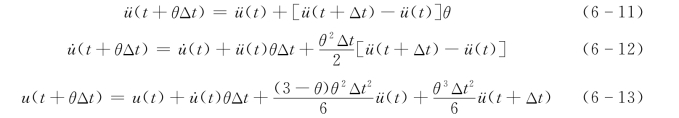
再由式（6-9）解得(www.daowen.com)

将式（6-14）的右端代入式 （6-11）、式 （6-12）及式 （6-13）中，并经整理后得

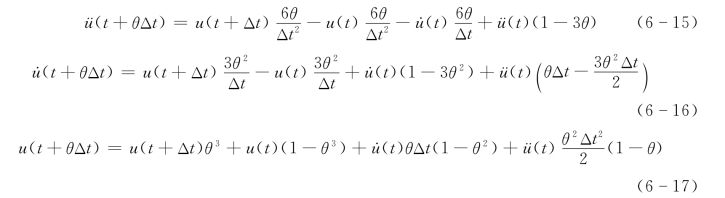
将式（6-15）～式 （6-17）代入式（6-18）有

整理后得

式中

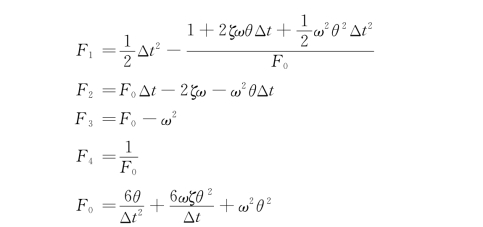
将式（6-19）代入式（6-14）得

再将式（6-20）代入式（6-8）后得

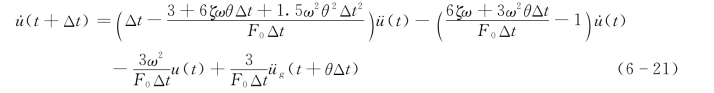
归纳一下，Wilson—θ法的计算步骤如下：

1）确定Δt及θ值。

2）输入离散的爆破地震动加速度记录。

3）计算常数F0、F1、F2、F3、F4。

4）由爆破地震动加速度曲线查出t+Δt时刻的地震动加速度值。

5）根据前一时刻t的ü（t）、u·（t）、u（t）值，由式 （6-19）、式 （6-20）、式 （6-21）计算t+Δt时刻的u（t+Δt）、ü（t+Δt）、u·（t+Δt）。

6）把上一步骤求出的加速度、速度、位移做为新一步的初始值，再重复步骤4）和5）。逐次推算下去就递推出整个爆破地震结构反应过程。

这里需要说明一点：Wilson—θ法虽然不论Δt取多大，它都是无条件稳定的，但是对解答的精度仍是有影响的，时间步长还是不宜取得过大。图6-3列出无阻尼单自由度体系由初位移产生的自由振动的计算结果。这种体系的自由振动解，自振周期，振幅均应为常量，但由于计算方法产生了误差，使周期延长，振幅衰减了。这相当于产生了附加阻尼，常称伪阻尼。图6-3表示出周期延长的百分比 （ΔT/T×100%）和振幅衰减的百分比 （ΔA/A×100%）。图6-3的曲线还表明，θ值过大，误差也显然增大，一般只取θ=1.4较合适，图中的曲线还表明误差随Δt/T的增大而增大，因此步长Δt应尽量取小些为好。如果取θ=1.4，Δt/T=0.1，由曲线查出周期会延长5.2%，振幅会衰减6.8%，这相当于增加阻尼比为1%的阻尼。这对于阻尼较大的结构（如重力坝，阻尼比10%，一般砖混建筑，阻尼比5%）是可以允许的，但对阻尼较小的结构 （如钢架、框架等，阻尼比1%～2%）附加了1%的阻尼就显得太大了。因此，对小阻尼结构，取Δt/T≤0.06更合适，计算精度对天然地震应足够了。但对于爆破地震，就不一定是这样了，因为爆破地震动的频率高，所用的步长Δt必须能够把爆破地震波的主频率的波形显示出来。直观地看，Δt最多只能取为Δt/Tp≤0.125，Tp为爆破地震波卓越周期（s），因此最好能满足Δt/Tp≤0.1。如果爆破地震波频率为单质点系的自振频率的10倍，则Tp=0.1T，这时Δt≤0.01T，T为结构的自振周期，可见高频率动力荷载作用，时程分析采用的时间步长应考虑荷载频率。

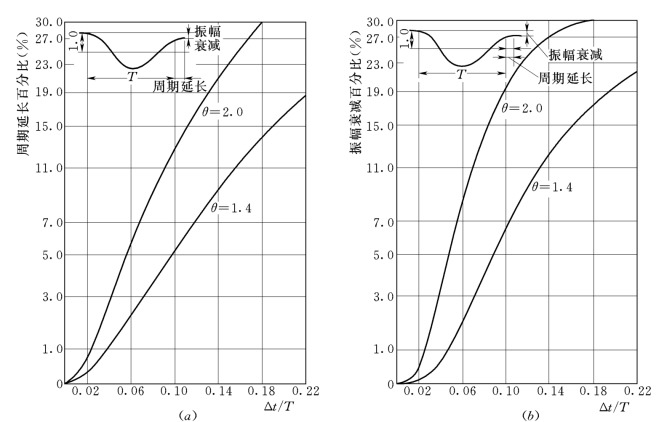
图6-3　周期延长和振幅衰减的百分率

（a）ΔT/T×100% ～Δt/T；（b）ΔA/A×100% ～Δt/T

（4）Newmark法。Newmark在线性加速度法假定的基础上，引入两个参数α及β，当这两个参数取某一值时，方法是无条件稳定的。Newmark假定速度与位移反应线按下列规律变化：

式中：α及β是Newmark引入的两个参数。

适当选取两个参数的值，可以使计算稳定，并达到要求的精度。经计算分析研究，当α＜1/2或α＞1/2时，都会产生伪阻尼，但前者取负值，后者取正值，伪阻尼正比于（α-1/2）。因此Newmark建议选择α=1/2，于是（6-22）变为

这是线性加速度法的基本公式之一。

对于β如何取值会使解法稳定、收敛，研究表明，β=1/4时，为无条件稳定法，计算精度也较好。实际上β=1/4时，相当于中点加速度法；β=1/6时，为线性加速度法；β=1/8时，相当于在Δt时段内加速度为阶形变化。

取β=1/4，式 （6-23）变成：

由式（6-25）解出ü（t+Δt）有

将式（6-26）代入式（6-24），可得出t+Δt时u·（t+Δt）的表达式为

将式（6-26）、式 （6-27）代入地震动激励的单质点系在t+Δt时刻的动力平衡方程式 （6-3），可求得u（t+Δt）的递推式，再代入式 （6-26）和式 （6-27），又求得ü（t+Δt）和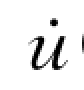（t+Δt）的递推式。反复由每一步长应用上述递推式，就可求出整个爆破地震动作用的全过程结构响应。